Solid-globule/coil transition

 For $\epsilon_g\gt$ the global minimum is orientationally ordered with a value of Q near to unity. Of course, this folded state corresponds to the free energy global minimum at zero temperature. However, as the temperature is increased there must come a point when a disordered higher entropy state, be it the globule or coil, becomes lowest in free energy, and the polymer loses its orientational order--it `melts'. This transition is signalled by a decrease in Q to a value close to zero, giving rise to a typical sigmoidal shape for the temperature dependence of Q [Figure 6a]. This transition is accompanied by a peak in the heat capacity [Figure 6b], and we use the position of this maximum to define the melting temperature of the polymer, T_m. (Alternative definitions, such as the temperature at which Q=0.5, give practically identical results). The transition also often involves a change in the radius of gyration, the sign and magnitude of this change depending on the stiffness of the polymer. For lower values of $\epsilon_g$ the transition to the dense globule, leads to a decrease in R_g, but at higher values of $\epsilon_g$ the transition to the coil leads to an increase in R_g ($\epsilon_g$=6$\epsilon$, 8$\epsilon$ in Figure 4a).

  

Figure 6: Behaviour of (a) Q and (b) C_v as a function of temperature and $\epsilon_g$ for N=343. Each line is labelled by the value of $\epsilon_g/\epsilon$.

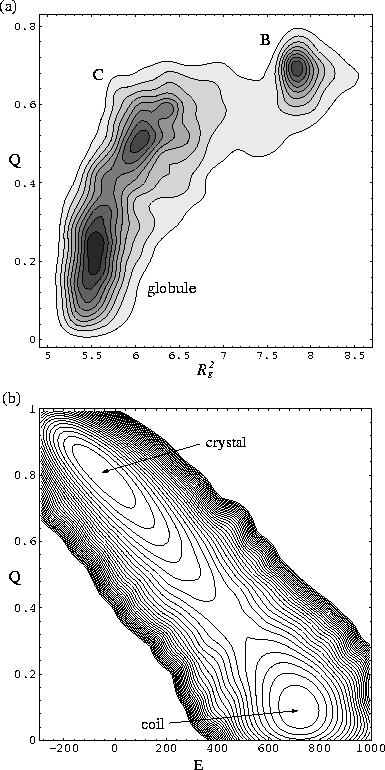
At temperatures in the transition region, as for the solid-solid transitions, dynamic coexistence of the ordered and disordered states is seen, leading to multimodal probability distributions (and free energy barriers) [Figure 7]. In the example shown in Figure 7a three states are seen. Structures based on the global minima B and C give rise to the two ordered states. The low value of Q ($\sim 0.5$) for the state associated with structure C is a reflection of the considerable disorder that can be present in the solid state at T_m. The peak with the lowest Q value is due to the disordered globule and an example of a polymer configuration that contributes to this peak is given in Figure 3c.

  

Figure 7: (a) Solid-globule coexistence observed for a 100-unit polymer with $\epsilon_g=\epsilon$ at $T=0.675\epsilon k^{-1}$. Two-dimensional probability distribution in Q and R_g². The labels B and C refer to the global minima of Table I on which the structure of the polymers contributing to the maxima are based. (b) Crystal-coil coexistence for a 343-unit polymer with $\epsilon_g=\epsilon$ at $T=3.45\epsilon k^{-1}$.Two-dimensional free energy profile in Q and E. The contours occur at intervals of 0.5kT above the global free energy minimum. The contours over 15kT above the global minimum are not plotted.

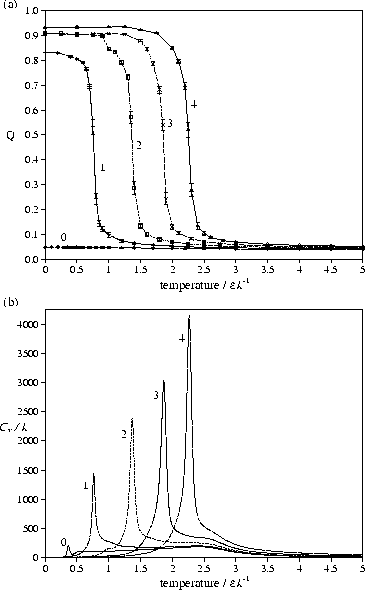
The effects of stiffness on this order-disorder transition can be seen from Figures 6 and 8. The temperature of the transition increases with stiffness, and at larger values of $\epsilon_g$ this increase is a little slower than linear. Accompanying this change is an increase in the height of the heat capacity peak, and therefore the latent heat of the transition. This increasing energy gap between the ordered and disordered states is a result of the increasing energetic penalty for the larger number of gauche bonds associated with the disordered state. As $T_m=\Delta E/\Delta S$, the dependence of the energy gap, $\Delta E$, on the stiffness is one of the main causes of the increase in T_m. This effect is reinforced by the changes in the entropy difference between ordered and disordered states, $\Delta S$:as $\epsilon_g$ increases the number of gauche bonds decreases, thus lowering the number of configurations contributing to the disordered state.

  

Figure 8: Phase diagram of the 343-unit polymer. The phase diagram is divided into regions by the values of T_m and $T_\theta$. The position of the heat capacity peak associated with collapse, T_c, has also been included. The solid lines with data points are simulation results, and the dotted line is from the simple theoretical calculation of T_m outlined in Section IIIB.

This behaviour is similar to simple liquids where decreasing the range of the potential leads to an increasing energy gap between solid and liquid because of the increasing energetic penalty for the disorder associated with the dispersion of nearest-neighbour distances in the liquid, thus playing an important role in the destabilization of the liquid phase.[34,35]

The respective roles of energy and entropy in the increase of T_m with stiffness can be investigated more quantitatively by approximating the free energy of the disordered state by that for the ideal coil. This is a reasonable approximation, since the ideal expression for n_g, $n_g^{ideal}=4N/(\exp(\beta\epsilon_g)+4)$,fits the simulation values for the coil, and for the globule, fairly closely. The free energy of an ideal coil A_ideal is  

$$A_{ideal}=-N k T\log\left( 1+ 4 \exp(-\beta \epsilon_g)\right).$$ (7)

Decomposing this expression into its energetic and entropic components showed that the increase in the energy with stiffness is the main contributor to the change in the free energy of the disordered state with stiffness, except at the higher temperatures relevant to the `melting' transition for larger values of $\epsilon_g$.

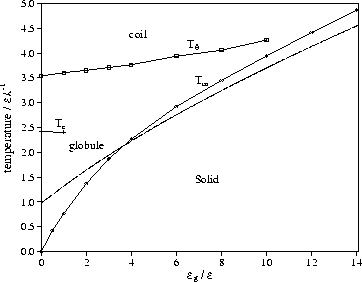
Use of Equation (7) also allows us to calculate a value of T_m if we approximate the free energy of the solid by only its energetic component [Equation (5)]. This simple calculation gives surprisingly good agreement with the simulation data [Figure 8], especially at larger $\epsilon_g$. It breaks down at low $\epsilon_g$, e.g. the prediction of a non-zero value of T_m at $\epsilon_g$=0, because Equation (7) is the free energy of a coil in the absence of any interactions; for the dense polymers at low $\epsilon_g$ and near to T_m, the polymer-polymer contacts make a significant contribution to the energy of the disordered state. The number of polymer-polymer contacts in the disordered polymer decreases significantly with increasing temperature, because of the larger entropy of less dense configurations. Therefore, Equation (7) becomes a better approximation to the free energy at higher temperatures, and thus provides a better description of melting at the higher temperatures relevant for larger $\epsilon_g$.

Our simulation results for T_m are also in qualitative agreement with theoretical results in which a more sophisticated treatment of the globule[15] gives the correct behaviour for T_m at low $\epsilon_g$. However, a drawback of the description of Doniach et al. is that the free energy of the coil per polymer unit is nonzero in the limit of large $\epsilon_g/kT$, causing T_m to reach an asymptotic value, rather than continuing to increase with $\epsilon_g$.

The increase in $\Delta E$ with stiffness also has an effect on the coexistence of ordered and disordered states. At large values of $\epsilon_g$ there is multimodality in the probability distribution for the energy as well as for the order parameter, because of larger free energy barriers between the states. In the example shown in Figure 7b there is a free energy barrier of 3.24 kT for passing from the crystal to the coil.

A consideration of the effect of size on the transition shows that as the polymer becomes longer the melting point becomes higher, and the transition becomes sharper with an increasing latent heat per monomer [Figure 9b]. This is consistent with the transition being the finite-size analogue of a first-order phase transition. T_m increases with size because the effect of the surface term (the N^2/3 term) in the energy of a crystallite [Equation (5)] diminishes with size. Moreover, as the coefficient of the surface term increases with $\epsilon_g$ (the higher aspect ratio crystallites have a larger surface area) the effects of size on T_m are more pronounced at larger $\epsilon_g$.

  

Figure 9: C_v/N as a function of size for (a) $\epsilon_g=0$. and (b) $\epsilon_g=3\epsilon$.

At $\epsilon_g$=0 the behaviour is qualitatively different because there is no energy difference between the orientationally ordered and disordered forms. As there are far fewer states that possess orientational order, they are never thermodynamically favoured and so there is no orientational order-disorder transition and Q always has a low value [Figure 6a]. Despite this, the polymers we studied do have a low temperature heat capacity peak at $T\sim 0.4\epsilon k^{-1}$ [Figure 9a]. This feature stems from a transition between the maximally compact cuboidal global minimum and a more spherical dense globule, and gives rise to bimodality in the canonical probability distribution of the energy. However, the latent heat per atom for the transition decreases with increasing size, indicating that the transition is not tending to a first-order phase transition in the bulk limit. Furthermore, the form of the heat capacity can be very different for sizes at which it is not possible to form complete cuboids.

The order-disorder transition observed by Zhou et al. was also for a fully flexible polymer.[10] However, as the model used was off-lattice, unlike in our model, there is the possibility of a first-order transition associated with the condensation of the monomers onto a lattice.