 |
To complete the phase diagram for our model polymer we estimated
![]() by making use of the scaling relations:
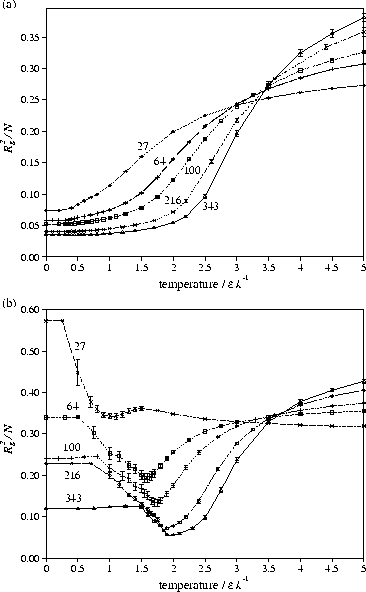
a series of plots of Rg2/N should all cross at
by making use of the scaling relations:
a series of plots of Rg2/N should all cross at ![]() .
However, due to finite size effects the value obtained by this method only approaches
the exact
.
However, due to finite size effects the value obtained by this method only approaches
the exact ![]() (from below) as
(from below) as ![]() .
For example, we estimate
.
For example, we estimate ![]() =0)=3.537 from the crossing
point of the lines for N=216 and 343,
whereas an accurate determination gives
=0)=3.537 from the crossing
point of the lines for N=216 and 343,
whereas an accurate determination gives ![]() =3.721.[3]
=3.721.[3]
Figure 8 shows that ![]() has only a weak dependence on
has only a weak dependence on
![]() .
Combined with the increase of Tm with
.
Combined with the increase of Tm with ![]() ,
this leads to the loss of the globular phase at
,
this leads to the loss of the globular phase at ![]() .
Above this value the polymer passes directly between the solid and the coil phases,
i.e. there is only one disordered phase.
An analogy can be made to the phase behaviour of simple atomic systems, with a correspondence
between the dense globule and the liquid and between the coil and the vapour.
For both systems the denser phase disappears as an interaction parameter is varied,
for polymers as the stiffness
is increased and for atomics systems as the range of the potential is decreased.[36]
.
Above this value the polymer passes directly between the solid and the coil phases,
i.e. there is only one disordered phase.
An analogy can be made to the phase behaviour of simple atomic systems, with a correspondence
between the dense globule and the liquid and between the coil and the vapour.
For both systems the denser phase disappears as an interaction parameter is varied,
for polymers as the stiffness
is increased and for atomics systems as the range of the potential is decreased.[36]
Our phase diagram is consistent with the work of Bastolla and Grassberger.
From simulations of polymers longer than those we study here,
they found that the globular phase disappears at ![]() .[16]
The phase diagrams is also very similar to the theoretical predictions of
Doniach et al. who estimate the loss of the globular phase to occur
at
.[16]
The phase diagrams is also very similar to the theoretical predictions of
Doniach et al. who estimate the loss of the globular phase to occur
at ![]() .[15]
However, they assumed that
.[15]
However, they assumed that ![]() is constant whereas both in ref. 16
and here a small increase with
is constant whereas both in ref. 16
and here a small increase with ![]() is observed.
is observed.
Precursors of the loss of the globular phase can be seen at ![]() .
These effects are due to finite size, and for smaller polymers they
occur at lower values of
.
These effects are due to finite size, and for smaller polymers they
occur at lower values of ![]() .
Firstly, the features in the heat capacity due to collapse become engulfed
by the peak due to melting. As the stiffness increases,
the collapse peak becomes only a shoulder and then
it disappears altogether [Figure 6b].
Secondly, on melting the polymer can pass directly from the solid to a low density
disordered state, albeit one where Rg2 scales less than linearly with size.
This effect can be seen for the 27-unit polymer at
.
Firstly, the features in the heat capacity due to collapse become engulfed
by the peak due to melting. As the stiffness increases,
the collapse peak becomes only a shoulder and then
it disappears altogether [Figure 6b].
Secondly, on melting the polymer can pass directly from the solid to a low density
disordered state, albeit one where Rg2 scales less than linearly with size.
This effect can be seen for the 27-unit polymer at ![]() [Figure 10],
and is also seen for longer polymers at larger values of
[Figure 10],
and is also seen for longer polymers at larger values of ![]() [Figure 4a].
It results from the expansion of sufficiently stiff and small polymers
with decreasing temperature, which is because the persistence length
becomes a significant fraction of the total length.
An estimate of the persistence length is given by the ratio N/ng, the
average length between gauche bonds,
[Figure 4a].
It results from the expansion of sufficiently stiff and small polymers
with decreasing temperature, which is because the persistence length
becomes a significant fraction of the total length.
An estimate of the persistence length is given by the ratio N/ng, the
average length between gauche bonds, ![]() .
.
Considerable theoretical effort has gone into studying the evolution of the coil-globule transition as the stiffness of the polymer is increased, see Refs. 37, 38 and references therein. The theories predict that the coil-globule transition is second order for flexible polymers (this has been confirmed by simulation[3]) but becomes first order as the stiffness increases. Due to the small size of the polymers we have simulated we are unable to determine the order of the transition accurately and so cannot test this prediction. However, the theories all assume a liquid-like dense phase; they neglect the possibility of an ordered dense phase, despite it being well known that the dense state of DNA, a stiff polymer, has hexagonal order.[39,40] It is clear from Figure 8 that for stiff polymers, the coil-globule transition is preempted by a coil-solid transition.
The difference in phase behaviour between flexible and stiff polymers can be easily understood. As a flexible polymer is cooled, the Boltzmann weight for polymer-polymer contacts increases and so the number of contacts increases, at a cost in the entropy of the polymer. The entropy cost derives from the fact that the polymer must bend back on itself in order for the units to be in contact. The increase in the number of contacts is continuous and so the radius of gyration of the polymer varies continuously -- the coil-globule transition is second order. However, bending a stiff polymer back on itself is more difficult, it costs both entropy and energy. This larger cost can be repaid if more than one pair of units is in contact, which is true if the two parts of the polymer run parallel to each other for several units. Of course, as the polymer is stiff the entropy cost for two parts of the polymer to run parallel for a number of units is small. The low energy configurations of a stiff polymer are those with long parts of the polymer parallel, see Section IIA. The energy gain is even larger if a number of parts of the polymer form a bundle,[41,42] e.g. if four parts of the polymer which are running parallel form a square bundle the energy is not twice but four times that of two parts running parallel. So, when the polymer is cooled below the point where the energy gain of bundles outweighs their entropy cost then these bundles proliferate and the radius of gyration drops suddenly -- the coil-solid transition is first order.
Our results can also be related to experiment.
The coil-globule transition of polystyrene, a flexible polymer, is continuous
and the globule is liquid-like.[37,43]
For DNA, an example of a stiff polymer,
a first-order transition has been observed between the coil and a
compact dense state,[39,44]
which has hexagonal order.[39,40]
The lattice model used here also has a continuous [3]
coil-globule transition when ![]() is small
and a first-order transition from a coil
to an ordered dense state when
is small
and a first-order transition from a coil
to an ordered dense state when ![]() is large.
It is thus able to reproduce the phenomenology of the existing experimental data.
However, we do not know of any examples where the three phases--coil, globule and
crystalline--predicted by our model to occur for semi-flexible polymers
have been experimentally observed.
is large.
It is thus able to reproduce the phenomenology of the existing experimental data.
However, we do not know of any examples where the three phases--coil, globule and
crystalline--predicted by our model to occur for semi-flexible polymers
have been experimentally observed.