Solid phase

In Table I the properties of the global minima for N=100 are given for the range of $\epsilon_g$ we consider in this study, and examples of these minima are illustrated in Figure 2. The shapes of the global minima agree well with that expected based on the analysis of section IIA. In the final column of Table I we have given the value of the stiffness for which a crystallite with the aspect ratio of the global minimum is expected to be lowest in energy based on Equation (4). This value generally lies in the middle of the range for which the structure is the global minimum. Most of the global minima have a degeneracy associated with the different possible ways of folding the chain back and forth. This degeneracy decreases as the chains become stiffer and the crystallites become more extended. For $\epsilon_g=0$ there is no constraint on n_g, and so the global minimum has a much larger degeneracy, and the majority of the isomers of the global minimum have no orientational order.

 

 

$$\epsilon_g^{min}/\epsilon \epsilon_g^{max}/\epsilon c/\protect\sqrt{ab} \epsilon_g^{opt}/\epsilon$$ n_pp n_g

A 136 38 0.000 0.375 1.118 0.059

B 133 30 0.375 0.500 1.563 0.281

C 129 22 0.500 0.833 2.406 0.703

D 124 16 0.833 2.167 3.704 1.352

E 111 10 2.167 3.500 6.804 2.902

F 97 6 3.500 12.000 12.500 5.750

  

Figure 2: Global minima of the 100-unit polymer at different values of $\epsilon_g$. The labels correspond to those in Table I.

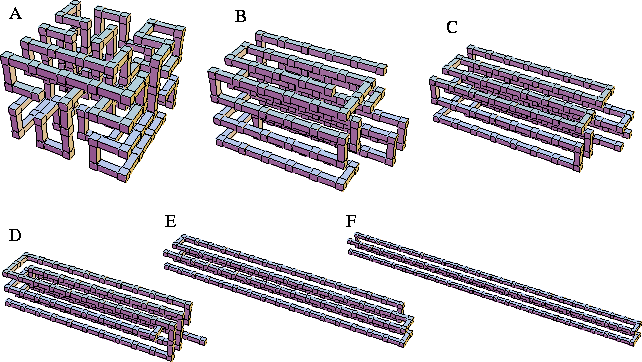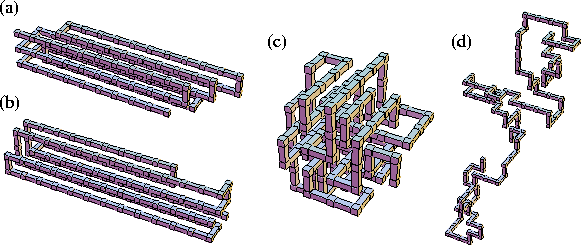
The global minimum is the free energy global minimum at zero temperature. However, as the temperature is increased it will become favourable to introduce defects into the structures. One of the mechanisms we commonly observed was through fluctuations in the lengths of the folds, moving in and out like the slide of a trombone. An example of such a structure is shown in Figure 3a. The generation of this type of defect is especially common at larger values of $\epsilon_g$ since it does not involve an increase of n_g.

  

Figure 3: Visualizations of various states of a 100-unit polymer. (a) A polymer based on structure D with some disorder in the stem lengths from a simulation at $T=0.9\epsilon k^{-1}$ and $\epsilon_g=2\epsilon$.(b) A folded structure with 8 stems that contributes to the middle peak of Figure 5b ($T=1.2\epsilon k^{-1}$, $\epsilon_g=3\epsilon$). (c) A typical configuration of the dense globule with R_g²=5.60 ($T=0.75\epsilon k^{-1}$, $\epsilon_g=\epsilon$). (d) A typical configuration of the coil with R_g²=38.91 ($T=5.0\epsilon k^{-1}$, $\epsilon_g=\epsilon$)

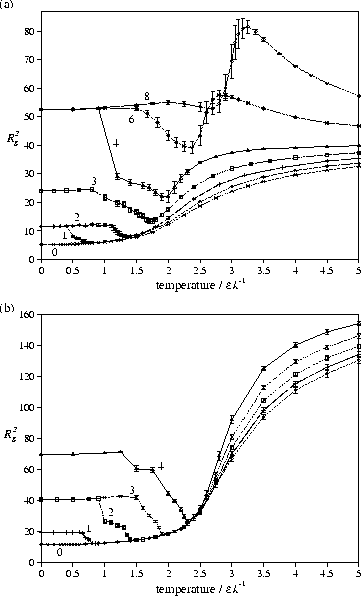
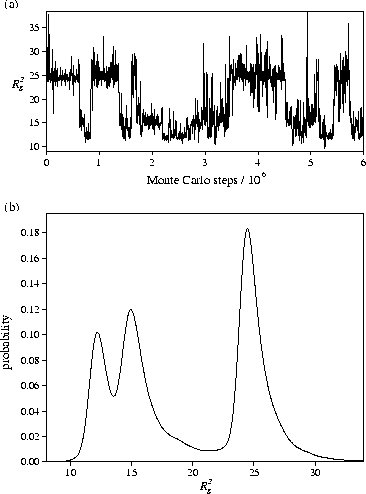
The dependency of the degeneracy, and therefore the entropy, on the aspect ratio of the crystallites raises the possibility of transitions to crystallites with a smaller aspect ratio as the temperature is increased. Indeed, this is usually what is seen and leads to the decrease of R_g² with temperature that is observed before melting [Figure 4]. At the centre of the transition, where the free energy of each crystallite is equal, ideally, the polymer would be seen to oscillate between the two forms [Figure 5a] during the simulation spending equal time in each. This `dynamic coexistence' of structures leads to a bimodal (or even multimodal if more than two forms are stable) distribution of R_g² [Figure 5b]. Since the Landau free energy is given by $A_L(q)=A-kT\log p_q(q)$, where A is the Helmholtz free energy and p_q(q) the canonical probability distribution for an order parameter q, the multimodality in R_g² implies that there are free energy barriers between the different crystallites. In the example shown in Figure 5, the peak with the highest value of R_g² corresponds to structures similar to the global minimum D, and the peak with the lowest value of R_g² have structures similar to C. The other peak consists of structures that have eight aligned stems, either in a $4\times 2$ array or a square array with one corner unoccupied [Figure 3b].

  

Figure 4: Behaviour of R_g² as a function of temperature and $\epsilon_g$ for (a) N=100 and (b) N=343. Each line is labelled by the value of $\epsilon_g/\epsilon$.

However, isomerization between the different forms often requires a large-scale change in structure, which is particularly difficult if these transitions occur at low temperature, where the free energy barriers to transitions are largest. With simulation techniques that only apply local moves, transitions between crystallites would be effectively impossible to observe and even with a technique such as configurational-bias Monte Carlo, where global moves are possible, transitions may be rare, particularly for the larger polymers in this study. This possible lack of ergodicity on the simulation time scales can lead occasionally to the abrupt jumps seen in R_g² (e.g. for N=100 at $\epsilon_g$=4$\epsilon$ and T=1$\epsilon k^{-1}$,and for N=343 at $\epsilon_g$=2$\epsilon$ and T=0.95$\epsilon k^{-1}$) rather than the smoother transition that would be expected if equilibrium values of R_g² were obtained.

  

Figure 5: Solid-solid coexistence observed for a 100-unit polymer with $\epsilon_g=3\epsilon$ at $T=1.2\epsilon k^{-1}$.(a) Fluctuations in R_g² during a 10 million step Monte Carlo run. (b) Probability distribution of R_g².

The differences in energy and entropy between crystallites of different aspect ratio are due to surface effects and so scale less than linearly with size. Therefore, these solid-solid transitions are not finite-size analogues of bulk first-order phase transitions.

Interestingly, this coexistence of polymers with different cuboidal shapes but the same basic structure bears some resemblance to the coexistence of cuboidal sodium chloride clusters that has recently been observed experimentally.[33] All the clusters have the rock-salt structure but the cuboids have different dimensions.