

Next: Simulation Techniques
Up: Methods
Previous: Methods
Home: Return to my homepage
In our model the polymer is represented by an N-unit self-avoiding walk
on a simple cubic lattice.
There is an attractive energy, 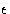 , between non-bonded polymer units on
adjacent lattice sites and an energetic penalty,
, between non-bonded polymer units on
adjacent lattice sites and an energetic penalty, 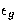 , for kinks in the chain.
The total energy is given by
, for kinks in the chain.
The total energy is given by
| 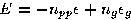 |
(1) |
where npp is the number of polymer-polymer contacts
and ng is the number of kinks or `gauche bonds' in the chain.
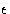 can be considered to be an effective interaction representing
the combined effects of polymer-polymer, polymer-solvent and solvent-solvent interactions,
and so our model is a simplified representation of a semi-flexible polymer in solution.
The behaviour of the polymer is controlled by the ratio
can be considered to be an effective interaction representing
the combined effects of polymer-polymer, polymer-solvent and solvent-solvent interactions,
and so our model is a simplified representation of a semi-flexible polymer in solution.
The behaviour of the polymer is controlled by the ratio 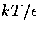 ;
large values can be considered as either high temperature or good solvent conditions,
and low values as low temperature or bad solvent conditions.
The parameter
;
large values can be considered as either high temperature or good solvent conditions,
and low values as low temperature or bad solvent conditions.
The parameter 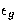 defines the stiffness of the chain. The polymer
chain is flexible at
defines the stiffness of the chain. The polymer
chain is flexible at 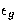 =0 and becomes stiffer as
=0 and becomes stiffer as 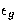 increases.
In this study we only consider
increases.
In this study we only consider 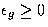 .
.
When 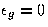 , this model corresponds to one originated by Orr[17]
and has been much used to study homopolymer
collapse.[3,14,18,19,20]
The system with positive
, this model corresponds to one originated by Orr[17]
and has been much used to study homopolymer
collapse.[3,14,18,19,20]
The system with positive 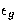 has been recently studied
theoretically by Doniach et al.[15] and using simulation by
Bastolla and Grassberger.[16]
In our work we pay special attention to the structural changes of a polymer of a specific size.
In this sense our work is complementary to that of ref. 16 which
focussed on the accurate mapping of the phase diagram.
has been recently studied
theoretically by Doniach et al.[15] and using simulation by
Bastolla and Grassberger.[16]
In our work we pay special attention to the structural changes of a polymer of a specific size.
In this sense our work is complementary to that of ref. 16 which
focussed on the accurate mapping of the phase diagram.
Our model was chosen because we wished to have the simplest model in
which we could understand the effects of stiffness, and because it gives
low energy states that have chain folds resembling those found in
lamellar homopolymer crystals.[21]
Similar structures have previously been seen in a diamond-lattice model
of semi-flexible polymers,[11,12,13]
and in molecular dynamics simulations of isolated polyethylene
chains.[22,23,24]
Particular mention should be made of the studies by Kolinski et al. on
the effect of chain stiffness on collapse[11,12,13]
since they found evidence for many of the phenomena that we explore systematically here.
The global minimum at a particular (positive) 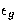 is
determined by a balance between maximizing npp
and minimizing ng.
If the polymer is able to form a structure that is a cuboid with
dimensions
is
determined by a balance between maximizing npp
and minimizing ng.
If the polymer is able to form a structure that is a cuboid with
dimensions 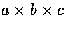 (N=abc), where
(N=abc), where
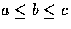 , then
, then
and
The structures that correspond to ng=ngmin have the polymer chain
folded back and forth along the longest dimension of the cuboid.
By minimizing the resulting expression for the energy one
finds that the lowest energy polymer configuration should have
| 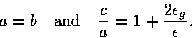 |
(4) |
Therefore, at 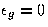 the ideal shape is a cube and for
positive
the ideal shape is a cube and for
positive 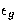 a cuboid extended in one direction,
the aspect ratio of which increases as the chain becomes stiffer.
As the ideal aspect ratio of the crystallite is independent of N,
its squared radius of gyration, Rg2, will scale as N2/3;
this scaling is the same as for the disordered collapsed globule.
a cuboid extended in one direction,
the aspect ratio of which increases as the chain becomes stiffer.
As the ideal aspect ratio of the crystallite is independent of N,
its squared radius of gyration, Rg2, will scale as N2/3;
this scaling is the same as for the disordered collapsed globule.
Substitution of the optimal dimensions of the cuboid [Equation (4)] into
Equations (1)-(3) gives a lower bound to the energy of the global minimum,
| 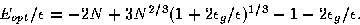 |
(5) |
However, at most sizes and values of 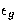 it is not possible
to form a cuboid with the optimal dimensions, and so the energy of the
global minimum will be higher than given by the above expression.
Nevertheless, it is easy to find the global minimum just
by considering the structures which most closely approximate this ideal shape.
it is not possible
to form a cuboid with the optimal dimensions, and so the energy of the
global minimum will be higher than given by the above expression.
Nevertheless, it is easy to find the global minimum just
by considering the structures which most closely approximate this ideal shape.


Next: Simulation Techniques
Up: Methods
Previous: Methods
Home: Return to my homepage
Jon Doye
1/31/1998
![]() , this model corresponds to one originated by Orr[17]
and has been much used to study homopolymer
collapse.[3,14,18,19,20]
The system with positive
, this model corresponds to one originated by Orr[17]
and has been much used to study homopolymer
collapse.[3,14,18,19,20]
The system with positive ![]() has been recently studied
theoretically by Doniach et al.[15] and using simulation by
Bastolla and Grassberger.[16]
In our work we pay special attention to the structural changes of a polymer of a specific size.
In this sense our work is complementary to that of ref. 16 which
focussed on the accurate mapping of the phase diagram.
has been recently studied
theoretically by Doniach et al.[15] and using simulation by
Bastolla and Grassberger.[16]
In our work we pay special attention to the structural changes of a polymer of a specific size.
In this sense our work is complementary to that of ref. 16 which
focussed on the accurate mapping of the phase diagram.
![]() is
determined by a balance between maximizing npp
and minimizing ng.
If the polymer is able to form a structure that is a cuboid with
dimensions
is
determined by a balance between maximizing npp
and minimizing ng.
If the polymer is able to form a structure that is a cuboid with
dimensions ![]() (N=abc), where
(N=abc), where
![]() , then
, then