Simulation Techniques

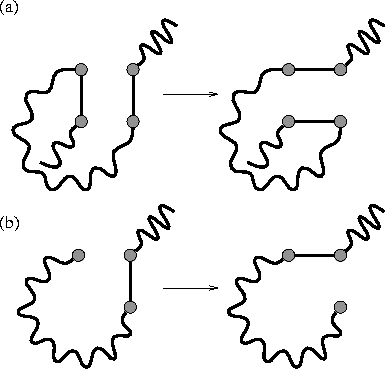
Recent advances in simulation techniques have made it possible to begin to study dense polymer systems. In particular, we use configurational-bias Monte Carlo[25] including moves in which a mid-section of the chain is regrown.[26] We also make occasional bond-flipping moves [Figure 1] which, although they do not change the shape of the volume occupied by the polymer, change the path of the polymer through that volume.[27,28] These moves speed up equilibration in the dense phases. The simulation method was tested by comparing to results obtained for $\epsilon_g=0$by exact enumeration.[29,30] Thermodynamic properties, such as the heat capacity, were calculated from the energy distributions of each run using the multi-histogram method.[31,32]

  

Figure 1: Bond-flipping moves. (a) Four-bond flip in which the mid-section of the chain is reordered. Moves of this type were only attempted if they preserved the integrity of the chain. (b) Two-bond flip which results in a new chain end. Only the bonds which change are explicitly depicted; other sections of the polymer are represented by wiggly lines.

The number of Monte Carlo steps used in our simulations was typically 4-30$\times 10^6$. The longer simulations were required for the larger polymers, especially at temperatures where two or more states coexisted. The sizes of the polymers we studied were N=27, 64, 100, 216, 343. These sizes are `magic numbers' for $\epsilon_g=0$, because compact cuboids of low aspect ratios can be formed at these sizes. In the presentation of our results we concentrate on polymers with N=100 and 343, the former because the smaller size allows for clear visualization of the structures of the different phases, and the latter because the effects of finite size will be smallest.

In order to monitor the orientational order within the polymer we devised an order parameter, Q, which is given by

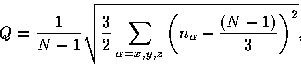$$Q={1\over N-1}\sqrt{{3\over 2}\sum_{\alpha=x,y,z} \left(n_\alpha-{(N-1)\over 3}\right)^2},$$ (6)

where $n_\alpha$ is the number of bonds in the direction $\alpha$ and (N-1)/3 is the expected value of $n_\alpha$ if the bonds are oriented isotropically. Q has a value of 1 if all the bonds are in the same direction, i.e. the polymer has a linear configuration, and a value of 0 if the bonds are oriented isotropically.