We start the simulation of BzAr ![]() in the canonical ensemble using
standard Metropolis Monte Carlo (MC) sampling with 10 million
steps at each temperature. The lowest
one-sided minimum (19|0) and the lowest two-sided structure, (7|5|7),
our lowest minimum, are used for the initial configuration in two separate runs.
The resulting canonical caloric curves (
in the canonical ensemble using
standard Metropolis Monte Carlo (MC) sampling with 10 million
steps at each temperature. The lowest
one-sided minimum (19|0) and the lowest two-sided structure, (7|5|7),
our lowest minimum, are used for the initial configuration in two separate runs.
The resulting canonical caloric curves ( ![]() vs. T) are
shown in Fig. 6.
vs. T) are
shown in Fig. 6.
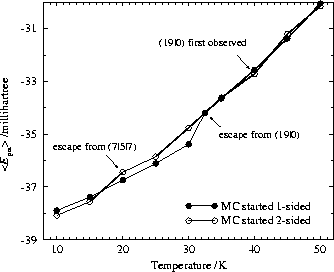
Although both caloric curves should represent the same ensemble they are inconsistent
below about 32.5K. The potential energy averages, ![]() ,
differ by up
to 2% and both curves show kinks at different temperatures. A
better understanding of these points can be achieved by periodic quenching of
the Metropolis walker to a local minimum, following Stillinger and
Weber [45].
,
differ by up
to 2% and both curves show kinks at different temperatures. A
better understanding of these points can be achieved by periodic quenching of
the Metropolis walker to a local minimum, following Stillinger and
Weber [45].
Each kink in the caloric curves corresponds to a first escape from a well-defined region of the PES, rather than a true melting process, indicating non-ergodic behaviour. For example, if we start from the one-sided (19|0) minimum then fully `solvated' two-sided structures are rarely sampled below 32.5K although they are lower in energy. On the other hand, starting from the (7|5|7) minimum prevents the Metropolis walker from sampling any one-sided structures in simulations of this length up to 40K although the associated region of configuration space is entropically significant. The only physical meaning that can be attached to the kinks in the caloric curves is the non-ergodicity of these simulations and the presence of relatively high barriers between the minima. Adams and Stratt [7] observed similar restrictions in their MC simulations although they found transitions between the one-sided and the two-sided regimes at lower temperatures (below 30K). This is not surprising because our SCM[1] potential parameters favour Ar-Ar binding compared to the OBJ[6]-like parameters used by Adams and Stratt.
We described in §iiC how the Jump-Walking Monte Carlo technique (JW) helps to overcome high transition barriers in MC simulations. This method can produce results which are much more ergodic, especially at low temperatures. At high temperatures JW and standard MC should give the same thermodynamic averages because even the standard Metropolis walker is able to access the whole of configuration space in a reasonable number of steps.
We first concentrate on high temperature simulations between 40K and 55K to
optimize the free
parameters in our JW implementation, i.e. the jump-probability
![]() , the dive-frequency
, the dive-frequency ![]() and the temperature difference
and the temperature difference
![]() between the parallel runs. Earlier studies [29] led us to
set
between the parallel runs. Earlier studies [29] led us to
set ![]() to 5K which gives reasonable jump-acceptance
rates of about 50%.
to 5K which gives reasonable jump-acceptance
rates of about 50%. ![]() and
and ![]() are more crucial
in preventing correlation effects between the parallel runs.
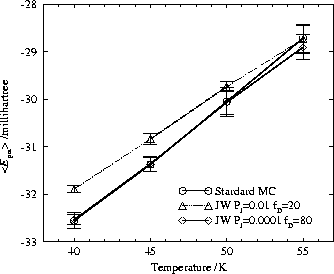
Fig. 7 shows how severely the
results are affected if the lower temperature Jumper follows the Diver too
closely through configuration space, i.e.
are more crucial
in preventing correlation effects between the parallel runs.
Fig. 7 shows how severely the
results are affected if the lower temperature Jumper follows the Diver too
closely through configuration space, i.e. ![]() is too high and/or
is too high and/or
![]() is too small. Here we also give the standard
deviation of the mean potential energy to explain the poor convergence at 55K.
The container radius of 25 bohr in these runs was not optimal.
Evaporation effects therefore disturbed the simulations making them less
efficient. However, for temperatures below 55K a large container size can be
used without problems for simulations of this length.
is too small. Here we also give the standard
deviation of the mean potential energy to explain the poor convergence at 55K.
The container radius of 25 bohr in these runs was not optimal.
Evaporation effects therefore disturbed the simulations making them less
efficient. However, for temperatures below 55K a large container size can be
used without problems for simulations of this length.
We choose ![]() and
and ![]() for our subsequent JW simulations.
Accordingly, configurations stored by the Diver survive with a half-life of
about
for our subsequent JW simulations.
Accordingly, configurations stored by the Diver survive with a half-life of
about ![]() steps with a buffer file of 1000 entries. We equilibrate a buffer over about
steps with a buffer file of 1000 entries. We equilibrate a buffer over about
![]() steps before the Jumper starts. Then, if we use a
50% jump-acceptance rate, about
3 structures from the higher temperature run are used during
each half-life period by the Jumper as new
positions in configuration space. Ergodicity should be
improved and indeed, the JW caloric curve in Fig. 8
differs from the standard MC results at lower temperatures (
steps before the Jumper starts. Then, if we use a
50% jump-acceptance rate, about
3 structures from the higher temperature run are used during
each half-life period by the Jumper as new
positions in configuration space. Ergodicity should be
improved and indeed, the JW caloric curve in Fig. 8
differs from the standard MC results at lower temperatures ( ![]() was set
to 4K below 30K).
was set
to 4K below 30K).
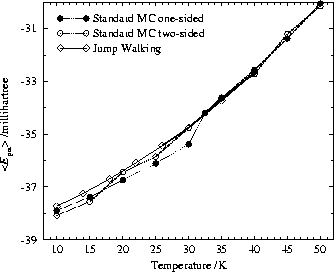
All kinks in the caloric curve disappear for the JW simulation.
In particular, we cannot see any obvious feature in the JW caloric curve that
could be interpreted as `melting' of the ![]() cluster - simulations of
neat
cluster - simulations of
neat ![]() clusters exhibit solid/liquid coexistence between 26K and
37K in terms of a short-time-averaged order parameter. [46]
There is no Van der Waals loop in the microcanonical caloric curve (presented
below) because the potential energy cannot be used as an order parameter to
distinguish between solid-like and liquid-like regions of phase space in this
cluster [4748].
clusters exhibit solid/liquid coexistence between 26K and
37K in terms of a short-time-averaged order parameter. [46]
There is no Van der Waals loop in the microcanonical caloric curve (presented
below) because the potential energy cannot be used as an order parameter to
distinguish between solid-like and liquid-like regions of phase space in this
cluster [4748].
The utility of the more ergodic JW sampling technique is further illustrated
if we use the relative configurational number of states,
![]() , from an
initially one-sided standard MC simulation in the histogram method proposed by
McDonald and Singer [16].
In Fig. 9 we show a caloric curve estimate calculated from
the potential energy histogram generated at 32.5K in an initially one-sided
simulation, i.e. at a temperature just above the
kink at about 30K. It results in a smooth curve interpolating the results from
JW and from initially two-sided standard MC simulations at 30K quite well,
despite the fact that we started from the (19|0) minimum.
Two-sided configurations seem to dominate in this temperature
range, although we find contributions from one-sided structures to the
ensemble averages above 35K in contrast to Adams and Stratt's [7]
observations. As before, the latter discrepancy might be due to the differences in the potential
parameters used. We obtained in our studies a variety of
very low-lying one-sided minima (§iiiA). However,
we also use five times as many MC steps as Adams and Stratt and we show below
that this is still insufficient to produce the correct transition
barrier for the initially two-sided standard MC simulations.
, from an
initially one-sided standard MC simulation in the histogram method proposed by
McDonald and Singer [16].
In Fig. 9 we show a caloric curve estimate calculated from
the potential energy histogram generated at 32.5K in an initially one-sided
simulation, i.e. at a temperature just above the
kink at about 30K. It results in a smooth curve interpolating the results from
JW and from initially two-sided standard MC simulations at 30K quite well,
despite the fact that we started from the (19|0) minimum.
Two-sided configurations seem to dominate in this temperature
range, although we find contributions from one-sided structures to the
ensemble averages above 35K in contrast to Adams and Stratt's [7]
observations. As before, the latter discrepancy might be due to the differences in the potential
parameters used. We obtained in our studies a variety of
very low-lying one-sided minima (§iiiA). However,
we also use five times as many MC steps as Adams and Stratt and we show below
that this is still insufficient to produce the correct transition
barrier for the initially two-sided standard MC simulations.
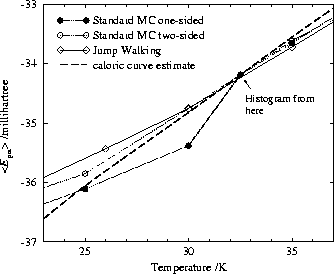
In Fig. 10 we plot some caloric curves calculated from the configurational number of states obtained by single standard MC runs at various temperatures. As in Fig. 9 it is easy to see that the caloric curve calculated in this way is only accurate in the vicinity of the temperature at which the histogram was generated. This is expected, since a single temperature simulation cannot give accurate statistics at energies which are rarely sampled. Tsai and Jordan reached a similar conclusion in their studies of homogeneous systems [29].
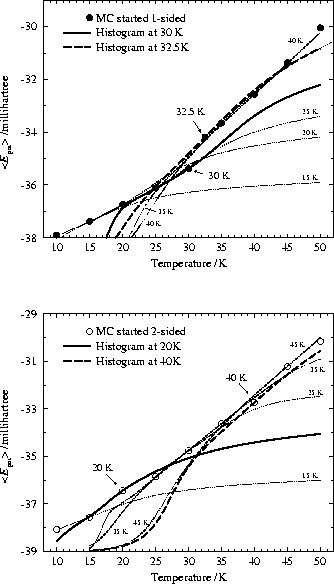
However, the results from the single histogram method help to explain systematic errors due to non-ergodic sampling. In our simulations which are trapped in one-sided configurations below 32.5K we obtain very different caloric curves from the configurational numbers of states calculated at 30K and 32.5 (Fig. 10 top). The drop in the average potential energy at 30K is not experienced by the more flexible Metropolis walker at 32.5K which can sample a much bigger, less restricted configuration space. In contrast, the simulation at 30K does not experience any contribution from two-sided structures which lie behind insurmountable barriers. The kink in the caloric curve from standard MC sampling started from the one-sided minimum has no other significance.
In simulations started from the two-sided minimum the caloric curves calculated by the histogram method exhibit a slightly different kind of discrepancy due to non-ergodicity at 20K and 40K (Fig. 10 bottom). At 20K, a temperature where non-ergodic sampling is very likely, the Metropolis walker escapes from the (7|5|7) regime but still cannot sample the configuration space experienced by the run at 25K. This is obvious since the calculated curves based on histograms collected at 25K, 30K and 35K interpolate a lower lying potential energy average at 20K. In contrast, the JW results presented in Fig. 8 imply that the standard MC sampling at 20K represents the canonical ensemble quite well whereas the 25K run seems to be trapped accidentally. The difference in interpretation is crucial for our MC simulations. The JW results suggest that larger standard MC runs are needed to improve convergence. However, if we try to elucidate the kink with the help of the single histogram method we find that the non-ergodicity is due to insurmountable barriers. This problem can only be solved by systematic changes in approach such as JW Monte Carlo.
We now consider the results at 40K, the lowest temperature where one-sided structures are observed in initially two-sided simulations of the given length. We can explain the small drop in the average potential energy if the one-sided regime becomes important entropically. However, the caloric curve obtained at 40K is significantly worse than the curves from the neighboaring sampling points. On looking at the regions visited by the 40K Metropolis walker using systematic quenching we found an unusual and accidental oversampling of one-sided structures compared to neighbouring temperatures. The latter show one-sided structures only on a smaller scale. The single histogram method helped us to find this inconsistency.
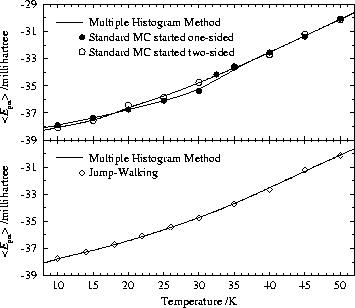
Finally, we employ a multiple histogram technique proposed by Weerasinghe and Amar [17] to combine the data gained from standard MC and from JW simulations (Fig. 11). Using the full histogram information results in smooth caloric curves which interpolate the discrete sampling points. Applying the convolution in Eq. 8 we calculate the relative number of states for an energy interval in phase space. Since we want to compare the resulting thermodynamic functions with our direct microcanonical simulations we take the integrals of motion corresponding to Molecular Dynamics into account (see Eq. 7).
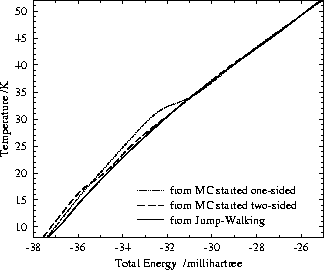
The absence of a Van der
Waals loop in the corresponding microcanonical caloric curve
(T vs. ![]() , see Fig. 12)
means that the canonical probability distribution of the total energy should be
unimodal over the temperature range in question [47].
We come
back to the microcanonical results in the next section. We also generate the corresponding
canonical partition function to obtain thermodynamic functions in this
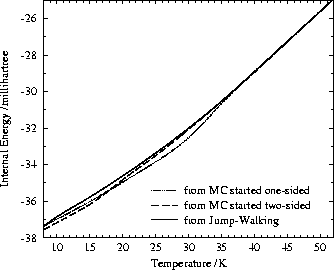
ensemble (Eq. 11). Hence, we plot in Fig. 13 the canonical
internal energy U(T) due to Eq. 12. As expected, the
functional shapes are very similar to the
original caloric curves shown in Fig. 11.
, see Fig. 12)
means that the canonical probability distribution of the total energy should be
unimodal over the temperature range in question [47].
We come
back to the microcanonical results in the next section. We also generate the corresponding
canonical partition function to obtain thermodynamic functions in this
ensemble (Eq. 11). Hence, we plot in Fig. 13 the canonical
internal energy U(T) due to Eq. 12. As expected, the
functional shapes are very similar to the
original caloric curves shown in Fig. 11.
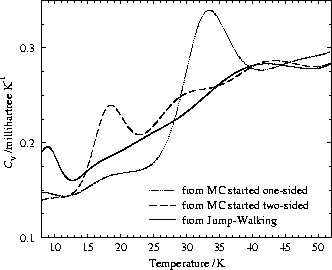
We estimate the heat capacity ![]() from the change in the internal
energy U(T) with respect to temperature (Eq. 13).
Calculation of
from the change in the internal
energy U(T) with respect to temperature (Eq. 13).
Calculation of ![]() from the potential energy
fluctuations (Eq. 14) results in almost perfectly matching curves in the
given temperature interval.
Therefore, numerical errors in the integration and differentiation routines for
the thermodynamic functions can be neglected. We expect rather poor estimates
around the lowest and the highest sampling points (10K and 50K) because of the
missing information for neighbouring temperatures. In fact, we use
additional standard Metropolis samplings at 5K in the multiple histogram method
for the one-sided and the two-sided results. However, we do not generate data
at 5K from Jump-Walking Monte Carlo and a non-physical maximum in the
from the potential energy
fluctuations (Eq. 14) results in almost perfectly matching curves in the
given temperature interval.
Therefore, numerical errors in the integration and differentiation routines for
the thermodynamic functions can be neglected. We expect rather poor estimates
around the lowest and the highest sampling points (10K and 50K) because of the
missing information for neighbouring temperatures. In fact, we use
additional standard Metropolis samplings at 5K in the multiple histogram method
for the one-sided and the two-sided results. However, we do not generate data
at 5K from Jump-Walking Monte Carlo and a non-physical maximum in the ![]() curve remains at about 9K. We obtained very similar errors for the
standard MC results before we included the histograms generated at 5K.
curve remains at about 9K. We obtained very similar errors for the
standard MC results before we included the histograms generated at 5K.
We did not investigate the possibility of multiple minima in Landau free energies or entropies to characterize melting in the present work. [48, 49] To identify such features, if they exist, it would be necessary to invent an order parameter to distinguish between the solid-like and liquid-like parts of phase space.