Simulation of the canonical ensemble (constant T, V and N) is commonly performed by the importance sampling scheme of Metropolis et al.[28] Monte Carlo (MC) points are in principle independent and could come from very different regions of configuration space as long as they belong to the correct distribution. In contrast to a Molecular Dynamics trajectory (compare §iiD), there is no equation of motion, i.e. no physical time connecting the sampled configurations. Metropolis' algorithm is one efficient way of sampling configuration space in the canonical ensemble. However, the energy-biased random walker is easily trapped in regions of configuration space that are surrounded by broad and high energy barriers. Hence, to improve ergodicity we use the Jump-Walking Monte Carlo (JW) approach proposed by Frantz, Freeman and Doll [15], as described below.
In JW Monte Carlo a Metropolis walker at lower
temperature (hereafter called a `Jumper') tries to jump to a
distribution generated by a higher temperature run (a `Diver') from time to time.
In sampling a canonical ensemble the jump acceptance probability
to jump from a lower temperature
Jumper-configuration, 
, to a Diver generated configuration, 
,
does not depend only
on the energy difference. It also depends on
the temperature difference between the Jumper and the Diver ensembles:
Hence, in JW both the temperature difference between the Jumper and the Diver runs and the maximum Cartesian displacement are crucial for efficiency.
Tsai and Jordan [29] applied JW to homogeneous clusters. They performed series of simulations decreasing in temperature. Every run stored some of the sampled configurations periodically and the following run was allowed to jump to these with an appropriate probability. Matro, Freeman and Topper [30] have recently developed an implementation which is similar to our approach. They used parallel computing software on multiple processors to realise the communication between individual runs and have applied this technique to study ammonium chloride clusters over a wide temperature range.
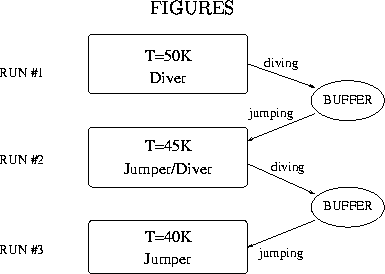
We use the Jump-Walking idea in a slightly different manner to deal
with relatively large systems in ORIENT 3.2 [27]. Here the storage of significant
parts of the
distribution is inconvenient and slow. Instead we perform parallel runs at
different temperatures which communicate all the time. To prevent correlation
effects, i.e. a Jumper following a Diver closely through configuration space, we
use communication buffers between all Jumper/Diver pairs (Fig. 1).
Periodically the
Diver writes its current configuration at a random position in the buffer which
contains many different entries. Hence relatively old configurations can survive
in the buffer and correlation is therefore minimized. After a short
equilibration time the Jumper is allowed to attempt jumps from time to time
to a configuration from the buffer. In practice we start different
temperature simulations on one or more computers simultaneously.
The highest temperature run only dives, the lowest only jumps, but all the
others can both dive and jump to the buffers from
the neighbouring temperatures. Ergodicity even for the lowest temperature is in
principle guaranteed, correlation effects can be minimized and the length of a
simulation is no longer restricted by storage problems. Correlation effects due
to buffer size, jump probability 
or dive frequency
are easily diagnosed by
comparison with standard MC results at high enough temperature.
We will discuss the influence of these parameters below. Here is defined
as the number of MC steps
taken between storage of the Diver configurations in the buffer.
In our simulations of BzAr 
the buffer size is fixed at 1000 configurations since a
bigger buffer does not appear to change the results. We fix
the constraining spherical container to a radius of 25 bohr.
This size should prevent the evaporation and external pressure effects
described by Tsai and Jordan [29]. The maximum Cartesian displacement
of the standard MC steps was adjusted dynamically to result in an acceptance rate of about
50%.
We can now apply the histogram method proposed by
McDonald and Singer [16] and extended by
e.g. Ferrenberg and Swendsen [31, 32] and
Bichara, Gaspard and Mathieu [33] to calculate
thermodynamic properties over a wider temperature range. In our
particular MC simulations we generate a normalised histogram
at
each sampling temperature 
. This histogram is equivalent to
,
where is the probability of finding the system with a potential
energy between 
and 
. Here 
is the number of microscopic states in configuration space in the above
potential energy interval and
is the configurational partition function. The probability distribution for a different value of T is calculated from
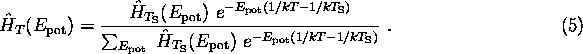
The ensemble average of an observable in configuration space,
,
is then found from
We will use the above method for observables dependent only on ,
but it can be generalised in a straightforward fashion as discussed below.
We normally
smoothed the histograms by fitting to an expansion of Gaussians which improves the accuracy
especially for the lower energy region. Five Gaussian functions are almost always
sufficient in the interpolation procedure.
However, systematic errors arise at temperatures very different from because
the quality of the histograms is poor far away from the sampled average
potential energy.
Various algorithms have been proposed to combine the histogram information
gained at different temperatures in a multiple histogram
method. [17, 29, 32, 33, 34]
We implemented the
approach of Weerasinghe and Amar [17]. This technique employs a
least-squares fit to find the relative number of configurational states,
, which strikes an optimized balance between the estimated
configurational densities for each value of . Different statistical
weights of the
histograms as used by Tsai and Jordan [29] are not taken into account
in the present work.
We convolute with the
density of kinetic states, 
,
which is known analytically from the volume of the 
-dimensional energy
hypersphere in momentum space as
Here is the number of degrees of freedom.
In our microcanonical Molecular
Dynamics simulations the overall linear and angular momenta are integrals
of motion. Hence, for comparison
is set to
and
we obtain 
, the number of microscopic
states in phase space with total
energy between E and 
, from the convolution [34, 35]
The different numbers of states are only known up to a multiplicative constant,
but all thermodynamical functions of interest can be calculated from the
relative values of . We consider for the microcanonical ensemble the
entropy,
and the temperature,
as functions of the total energy. We compare these quantities with the direct Molecular Dynamics results. For the canonical ensemble we use the canonical partition function,
to calculate the canonical internal energy,
and the canonical heat capacity,
as functions of temperature. To test the initial Monte Carlo results obtained from the multiple histogram method we also estimate the specific heat from the fluctuations of the potential energy: [29, 36, 37]
where the last term represents the kinetic contribution.
We do not show error bars in most of our diagrams. However, all averages of the potential energy are converged to 1% or better and the numerical derivatives and integrals employed are of much higher accuracy. More careful error estimates should include correlation time effects [29] but we have not gone to such lengths in this paper. Correlation between the Molecular Dynamics integration steps is actually very small because the propagator we use favours rather large time steps.
