One reason suggested for the polytetrahedral character of liquids
is the fact that the regular tetrahedron represents the densest possible local packing of
spheres. However, the regular tetrahedron cannot be used to pack all space.
This is illustrated in Figure 2.3; if five regular tetrahedra are packed around a common edge,
there remains a small gap of ![]() ,
and if twenty regular tetrahedra are packed around a common vertex the
gaps amount to a solid angle of 1.54 steradians, which is equivalent to 2.79 additional regular tetrahedra.
This incompatibility of the preferred short-range order with a global
packing is termed `frustration'.
As a consequence of this frustration,
close packing, which consists of a mixture of regular tetrahedra and octahedra, rather
than a polytetrahedral packing, is the densest packing of all space.
Furthermore, a polytetrahedral packing of space must involve tetrahedra that are distorted from
regularity, leading to local strains and a range of nearest-neighbour distances.
Polytetrahedral structure therefore underlies the larger strain energies in the liquid phase and the
dependence of liquid stability on the range of the potential.
,
and if twenty regular tetrahedra are packed around a common vertex the
gaps amount to a solid angle of 1.54 steradians, which is equivalent to 2.79 additional regular tetrahedra.
This incompatibility of the preferred short-range order with a global
packing is termed `frustration'.
As a consequence of this frustration,
close packing, which consists of a mixture of regular tetrahedra and octahedra, rather
than a polytetrahedral packing, is the densest packing of all space.
Furthermore, a polytetrahedral packing of space must involve tetrahedra that are distorted from
regularity, leading to local strains and a range of nearest-neighbour distances.
Polytetrahedral structure therefore underlies the larger strain energies in the liquid phase and the
dependence of liquid stability on the range of the potential.
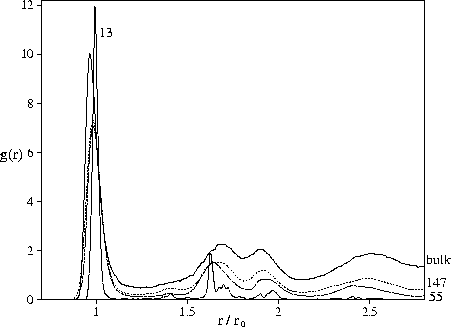
The radial distribution functions shown in Figure 4.7 provide evidence for
the polytetrahedral character of the liquid minima through the absence of a peak at ![]() ,which is the signature of the octahedra that occur in closed-packed structures, and the split second peak.
The split second peak of the structure factor, which is a common feature of supercooled liquids and glasses,
has also been shown to be a consequence of polytetrahedral order[196].
,which is the signature of the octahedra that occur in closed-packed structures, and the split second peak.
The split second peak of the structure factor, which is a common feature of supercooled liquids and glasses,
has also been shown to be a consequence of polytetrahedral order[196].
 |
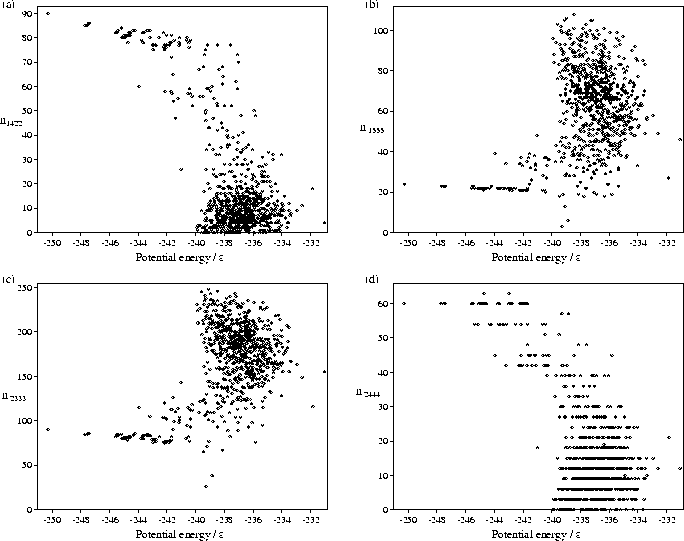
We have also performed a common-neighbour analysis[149,195,197] for our samples of minima. This analysis assigns four indices ijkl to each pair of atoms which have common neighbours, and provides a description of the local environment of the pair. Firstly, those pairs of atoms which are separated by less than a physically reasonable cutoff distance are designated nearest neighbours. We have simply set the cutoff equal to the minimum between the first and second peaks in the liquid radial distribution function. For those pairs of atoms which are nearest neighbours i is assigned the value 1. For those pairs of atoms which are not nearest neighbours but which have common neighbours i is assigned the value 2. The index j specifies the number of neighbours common to both atoms. The index k specifies the number of nearest-neighbour bonds between the common neighbours. The index l specifies the longest continuous chain formed by the k bonds between common neighbours.
This analysis allows differentiation between different types of local order.
In particular, 1421, 1422 and 2444 (an octahedron) pairs are associated with close packing;
1555 (a pentagonal bipyramid), and 2333 (a trigonal bipyramid) pairs are associated with polytetrahedral packing.
Scatter plots of some of these indices for the M55 minima are shown in Figure 4.8.
The plots clearly show that the higher energy
`liquid-like' minima have a larger proportion of polytetrahedral pairs and fewer close-packed environments.
Furthermore, a common neighbour analysis allows the properties associated with certain local environments
to be found.
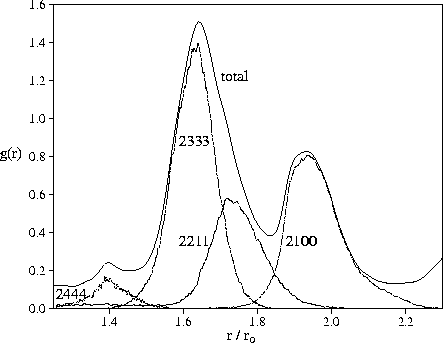
In Figure 4.9, we decompose the second peak of the radial distribution function for M55
according to the types of common neighbour pairs.
The first subpeak is clearly due to trigonal bipyramids (2333 pairs)
and the 2nd subpeak to linear configurations (2100 pairs).
The split second peak is therefore an indicator of polytetrahedral order.
The effect of 2111 pairs (a pair of atoms at the apices of a rhombus) is smaller
than in the case of bulk hard sphere systems[197].
 |
 |
The constraints that lead to the frustration inherent in polytetrahedral packings of
3-dimensional Euclidean space can be altered by introducing curvature into the space.
In fact, in a space of appropriate positive curvature
a perfect tetrahedral packing can be achieved in which there is no frustration
and each atom is icosahedrally coordinated.
The resulting structure is that of polytope ![]() which consists of a regular arrangement
of 120 atoms on the 3-dimensional hypersurface of a 4-dimensional hypersphere[198,199].
The effects of this lack of frustration have been well illustrated in work by Straley[200,201]
who compared the melting and crystallization of an fcc crystal in flat space,
with that of polytope
which consists of a regular arrangement
of 120 atoms on the 3-dimensional hypersurface of a 4-dimensional hypersphere[198,199].
The effects of this lack of frustration have been well illustrated in work by Straley[200,201]
who compared the melting and crystallization of an fcc crystal in flat space,
with that of polytope ![]() .In particular, the kinetics of crystallization from a liquid are much easier on the 4D hypersphere.
In line with Frank's original suggestion concerning the supercooling of metallic liquids,
this result has been interpreted as showing that the solid and liquid on
the 4D hypersphere have the same kind of order, i.e. both are polytetrahedral.
Therefore, it provides further evidence for the polytetrahedral nature of the liquid phase.
.In particular, the kinetics of crystallization from a liquid are much easier on the 4D hypersphere.
In line with Frank's original suggestion concerning the supercooling of metallic liquids,
this result has been interpreted as showing that the solid and liquid on
the 4D hypersphere have the same kind of order, i.e. both are polytetrahedral.
Therefore, it provides further evidence for the polytetrahedral nature of the liquid phase.
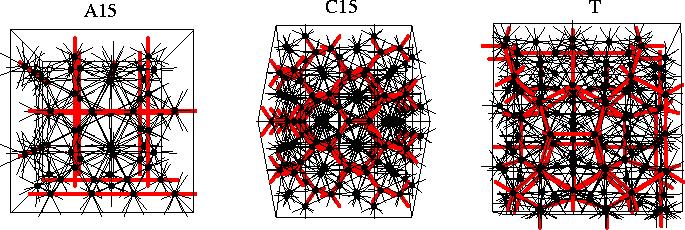 |
Nelson has shown that in the transformation of regular polytetrahedral packings from curved to Euclidean space disclination lines must be introduced[198,199]. If these disclination lines are arrayed periodically one obtains crystalline structures called Frank-Kasper phases[202,203]. If the disclination lines have a disordered arrangement it has been suggested that one obtains structures typical of liquids and glasses. The disclination networks for three types of Frank-Kasper phase, termed the A15, C15 and T phases[204], are illustrated in Figure 4.10; the disclinations of the T phase form an interconnected network of dodecahedra. The Frank-Kasper phases are sometimes referred to as tetrahedrally close-packed because of their polytetrahedral nature and are closely related to many icosahedral quasicrystals[205]. The known examples are generally alloys where some of the frustration is relieved by the different atomic sizes. It has been suggested that a mixture of different-sized fullerenes might be able to form a Frank-Kasper phase and even quasicrystals[206]. However, this seems unlikely given the short-ranged character of fullerene potentials (§2.2.1)--the structures must still be able to accommodate some strain. Interestingly, the dual of the A15 Frank-Kasper phase (Figure 4.10) has recently been found to divide space into equal cells of minimum surface area[207], overturning Kelvin's proposed optimal structure[208] which stood for over a century.
On the unfrustrated 4D hypersphere there must be an equal number of positive and negative disclinations.
However, as a consequence of the residual gap that occurs when five regular tetrahedra share
a common edge in Euclidean space (Figure 2.3a),
there must be an excess of negative disclinations[198,199].
For example, the Frank-Kasper phases involve only negative disclinations (Figure 4.10).
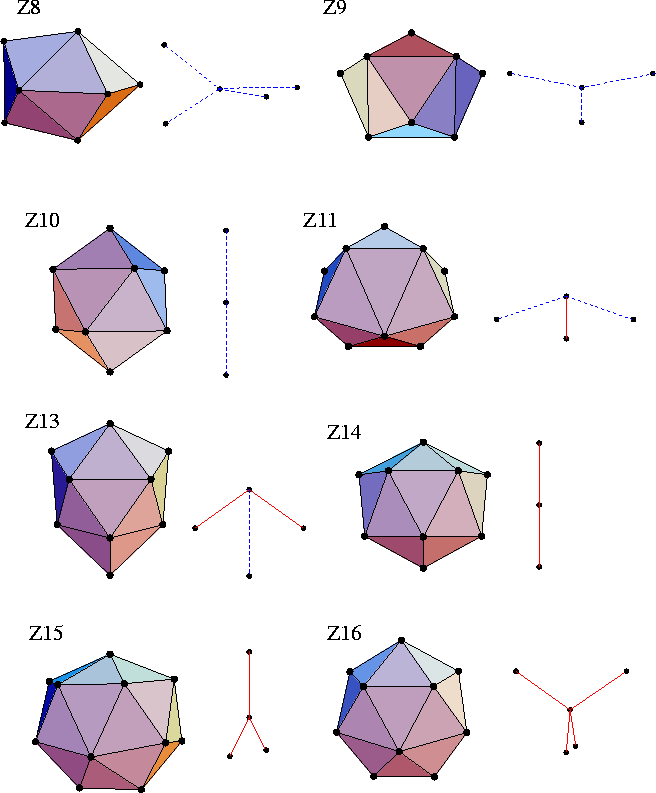
If an atom is 12-coordinate by the Voronoi procedure, it can be free of disclinations.
However, atoms that have a different coordination number must have disclinations passing through them.
Using Euler's rule and the fact that the coordination polyhedra are deltahedral,
one can deduce the coordination polyhedra which involve the minimum number of disclinations.
These polyhedra are termed the Kasper polyhedra, and are illustrated in Figure 4.11.
(They are denoted by ZN, where N is the coordination number.)
For example, apart from icosahedra the A15 Frank-Kasper phase (Figure 4.10)
involves only Z14 Kasper polyhedra,
and the C15 structure (Figure 4.10) involves only Z16 Kasper polyhedra.
 |
We can also understand the range-dependence of the energy of the `liquid-like' minima
by considering the energetics of disclination lines.
The strains associated with the disclination lines are most easily accommodated in
systems bound by long-ranged forces. In fact the
clusters which correspond to the Kasper polyhedra Z10, Z13, Z14 and Z15 are the
global minima for the Morse potential at ![]() , and those that correspond to
Z11 and Z16 are the second lowest energy stationary points of their size (§2.3.4).
As the range of the potential decreases the energetic penalty for the
local strains associated with the lines increases, causing destabilization of the liquid phase.
, and those that correspond to
Z11 and Z16 are the second lowest energy stationary points of their size (§2.3.4).
As the range of the potential decreases the energetic penalty for the
local strains associated with the lines increases, causing destabilization of the liquid phase.
In Nelson's original paper outlining his disordered disclination model for liquid structure, he
gives a schematic diagram of such an arrangement[198,199].
The sketch involves only Kasper polyhedra; long disclination lines,
mediated by the Z10 and Z14 Kasper polyhedra, thread through the icosahedrally coordinated medium,
and the other Kasper polyhedra act as nodes for the disclinations.
Surprisingly, no-one, as far as we are aware, has attempted to verify this model
by visualization of the disclination network. However, results from the statistical analysis of
Voronoi polyhedra indicate that the density of disclinations is higher than this
picture would suggest; for example, in Finney's analysis of dense random packings of hard spheres
only 40% of the faces of the Voronoi polyhedra are
pentagonal, thus indicating that for this system about 60% of bonds involve disclinations
including a significant number of ![]() -type[209].
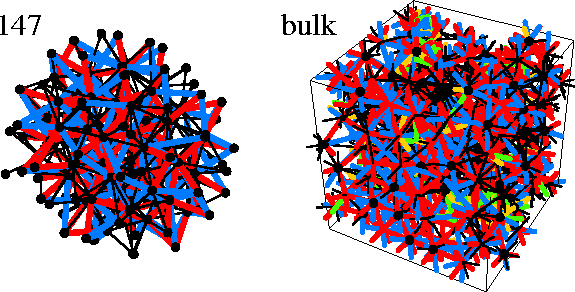
In part of Figure 4.12 we show the disclination network for a typical bulk liquid minimum;
the disclination density is so high that the result is an unintelligible mass of lines.
Typically, for the minima we analysed, only about 10% of the atoms have an icosahedral or
Kasper polyhedral coordination shell, in contrast to Nelson's original picture.
However, the disclination density is likely to be lower for simple binary liquids
where the size of the atoms are chosen to reduce the frustration. It is for such a system that
the most striking examples of local icosahedral order have been obtained[195].
-type[209].
In part of Figure 4.12 we show the disclination network for a typical bulk liquid minimum;
the disclination density is so high that the result is an unintelligible mass of lines.
Typically, for the minima we analysed, only about 10% of the atoms have an icosahedral or
Kasper polyhedral coordination shell, in contrast to Nelson's original picture.
However, the disclination density is likely to be lower for simple binary liquids
where the size of the atoms are chosen to reduce the frustration. It is for such a system that
the most striking examples of local icosahedral order have been obtained[195].
 |
As we saw in Chapter 2,
the lowest energy structures of clusters at low ![]() are polytetrahedral.
Furthermore, Figure 4.4 shows that for M55 and M147
these structures correlate with low energy liquid-like minima.
Therefore, Figures 2.10 and 2.18 allow us to see how
polytetrahedral packings and liquid structure evolve with size.
At small sizes is it possible to accommodate the strain that is associated with
the bridging of the `gaps' that occur in a disclination-free packing of
regular tetrahedra (Figure 2.3).
Anti-Mackay growth on the 13-atom icosahedron gives disclination-free
polytetrahedral structures up to 45.
Above this size disclinations have to be introduced.
Whilst the disclination density is still small, ordered arrangements of the
disclinations, which are fragments of Frank-Kasper phases, can form at some sizes
(N=51-53, 56, 57, 59-61, 70, and 74).
However, as the size increases the structures become progressively
more disordered.
By the time M147 is reached the cluster is a mass of interconnected disclinations (Figure 4.12);
only 53% of the interior bonds of 147A are disclination-free.
are polytetrahedral.
Furthermore, Figure 4.4 shows that for M55 and M147
these structures correlate with low energy liquid-like minima.
Therefore, Figures 2.10 and 2.18 allow us to see how
polytetrahedral packings and liquid structure evolve with size.
At small sizes is it possible to accommodate the strain that is associated with
the bridging of the `gaps' that occur in a disclination-free packing of
regular tetrahedra (Figure 2.3).
Anti-Mackay growth on the 13-atom icosahedron gives disclination-free
polytetrahedral structures up to 45.
Above this size disclinations have to be introduced.
Whilst the disclination density is still small, ordered arrangements of the
disclinations, which are fragments of Frank-Kasper phases, can form at some sizes
(N=51-53, 56, 57, 59-61, 70, and 74).
However, as the size increases the structures become progressively
more disordered.
By the time M147 is reached the cluster is a mass of interconnected disclinations (Figure 4.12);
only 53% of the interior bonds of 147A are disclination-free.
Why should liquids have a polytetrahedral structure though? Why is liquid structure not more like a highly defective version of the solid? Stillinger and Weber have used a model partition function to show that if defects of a body-centred-cubic lattice interact, then a first-order melting transition can occur which is associated with the condensation of a `gas' of defects[210]. One of the common reasons suggested for the polytetrahedral character of liquids is the energetic favourability of local icosahedral order. This argument dates back to Frank and his comparison of icosahedral and cuboctahedral 13-atom clusters that we mentioned above. However, this argument contains a fallacy. The reason for the lower energy of the icosahedron is primarily a surface effect; each surface atom is six-coordinate for the icosahedron and five-coordinate for the cuboctahedron. The actual energy of the interior atom will be slightly higher for the icosahedron, because the radial nearest-neighbour distance is slightly compressed with respect to the ideal. Furthermore, as has been pointed out by Clarke and Jonsson[197], an energetic argument cannot account for the fact that dense random packings of hard spheres (where all configurations have the same energy) show significant polytetrahedral order. Another observation is the fact that the tetrahedron has the greatest local density. However, if one considers the density of an icosahedron, the distortion required to bridge the gaps of Figure 2.3b leads to a decrease in density to such an extent that a cuboctahedron is denser[211].
What then is the reason for the polytetrahedral structure of liquids?
To answer this question one needs to realize that polytetrahedral packings should be compared
not to the close-packed solid, but to other states that could possibly mediate a melting transition.
The number of ways of arranging disclination lines in a polytetrahedral packing
or of introducing disclination lines into polytope ![]() to bring the curvature nearer to that of
flat space is huge[212].
Consequently, there is a large configurational entropy associated with the set of all polytetrahedral states.
Yet they are also fairly dense, and depending on the range of the potential, can be fairly low in energy.
It is the combination of these three factors (or the first two in the case of hard spheres)
which underlies the favourability of polytetrahedral order.
to bring the curvature nearer to that of
flat space is huge[212].
Consequently, there is a large configurational entropy associated with the set of all polytetrahedral states.
Yet they are also fairly dense, and depending on the range of the potential, can be fairly low in energy.
It is the combination of these three factors (or the first two in the case of hard spheres)
which underlies the favourability of polytetrahedral order.
One of the fundamental questions of cluster science is when and how bulk-like character develops.
The answer of course depends on the property considered. For instance, the structure of
solid-like clusters only becomes bulk-like at large sizes for many systems, especially for those
clusters with a long-ranged potential[213]--sodium clusters are icosahedral up
to at least ![]() atoms[53] even though the bulk structure is body-centred cubic.
In contrast, our results show that bulk-like liquid structure can develop at rather
small cluster sizes. This is suggested by the similar energetic destabilization of the
bulk, M55 and M147 `liquid-like' minima and by the clear similarity of their radial distribution functions
(Figure 4.7).
The only significant difference is the uniformly smaller value of the cluster radial distribution function,
and this is simply due to the finite size. The peaks in the M13 radial distribution function are
at a similar position to the larger clusters but are much sharper because at this size the
effects of frustration are small.
The similarity of bulk and cluster radial distribution functions can easily be
understood within the polytetrahedral model of liquid structure.
Given the favourability of polytetrahedral structure for small clusters and the rapid increase in disclination
density with size, it is not surprising that bulk-like liquid character is seen at small sizes.
atoms[53] even though the bulk structure is body-centred cubic.
In contrast, our results show that bulk-like liquid structure can develop at rather
small cluster sizes. This is suggested by the similar energetic destabilization of the
bulk, M55 and M147 `liquid-like' minima and by the clear similarity of their radial distribution functions
(Figure 4.7).
The only significant difference is the uniformly smaller value of the cluster radial distribution function,
and this is simply due to the finite size. The peaks in the M13 radial distribution function are
at a similar position to the larger clusters but are much sharper because at this size the
effects of frustration are small.
The similarity of bulk and cluster radial distribution functions can easily be
understood within the polytetrahedral model of liquid structure.
Given the favourability of polytetrahedral structure for small clusters and the rapid increase in disclination
density with size, it is not surprising that bulk-like liquid character is seen at small sizes.
As the size of the Mackay icosahedron increases, the polytetrahedral character decreases and the close-packed character increases. This can explain some of the differences in the correlation diagrams of the two larger clusters (Figure 4.4). For the 55-atom cluster the distinction between the top of the band of defective icosahedral structures and the band of `liquid-like' minima is unclear because of the greater structural similarity of the solid and the liquid at this small size. The energetic separation of these two bands of minima becomes larger as the number of atoms increases, giving the correlation diagram of M147 the two-state character expected for a system that undergoes a first-order phase transition.
Another related effect is the energetic differentiation between the minima found by
quenching from a glass or supercooled liquid and from the liquid that occurs for M147.
Structure 147A (Figures 4.5 and 4.12), the global minimum at ![]() ,was found from the collapse of one of the `liquid-like' minima of our sample.
It can be seen in Figure 4.4 that at
,was found from the collapse of one of the `liquid-like' minima of our sample.
It can be seen in Figure 4.4 that at ![]() there is an energy gap between this
and the next lowest energy minimum that we found.
This is not because there are no minima in between.
In fact, we found that this gap was an artifact of our sample;
147A is actually at the bottom of a band of minima which is almost continuous in energy.
The clue to the nature of structure 147A came when it was reoptimized for ascending values of
there is an energy gap between this
and the next lowest energy minimum that we found.
This is not because there are no minima in between.
In fact, we found that this gap was an artifact of our sample;
147A is actually at the bottom of a band of minima which is almost continuous in energy.
The clue to the nature of structure 147A came when it was reoptimized for ascending values of ![]() ;
the resulting line runs parallel to but below the main `liquid-like' band, indicating that it is of
essentially similar structure to the `liquid-like' minima. This suggested that 147A was one of a set of minima
that for a medium-ranged potential comes from a glassy region of phase space;
these states are essentially just the low energy continuation of the `liquid-like'
band of minima but are never observed at equilibrium because of their smaller entropy.
This hypothesis was confirmed by quenching from a supercooled M147 liquid at
;
the resulting line runs parallel to but below the main `liquid-like' band, indicating that it is of
essentially similar structure to the `liquid-like' minima. This suggested that 147A was one of a set of minima
that for a medium-ranged potential comes from a glassy region of phase space;
these states are essentially just the low energy continuation of the `liquid-like'
band of minima but are never observed at equilibrium because of their smaller entropy.
This hypothesis was confirmed by quenching from a supercooled M147 liquid at ![]() .
The resulting minima were lower in energy than the `liquid-like' band, but as for 147A ran parallel
to the `liquid-like' band in the correlation diagram.
.
The resulting minima were lower in energy than the `liquid-like' band, but as for 147A ran parallel
to the `liquid-like' band in the correlation diagram.