


Next: Thermodynamic Properties
Up: Anharmonicity
Previous: The effect of transition
Home: Return to my homepage
Here we follow the method of Haarhoff[164,166] to calculate
an anharmonic correction term to the density of states.
The energy levels for a Morse oscillator are given by
| 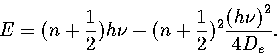 |
(3.17) |
This quadratic can be solved for n.
The root corresponding to a bound state is
| 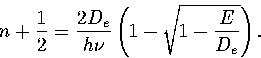 |
(3.18) |
Assuming n is continuous and differentiating with respect to E gives a classical
density of states,
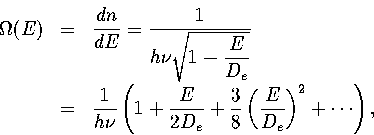
(3.19)
where the square root has been expanded binomially.
The expansion is valid if E/De is small.
The first term in the series is the harmonic term.
The full series will diverge as 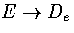 .
This divergence is the correct behaviour for the Morse oscillator,
but for the case of a cluster isomerization
.
This divergence is the correct behaviour for the Morse oscillator,
but for the case of a cluster isomerization 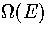 remains finite
as
remains finite
as 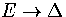 from below, where
from below, where 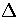 is the barrier height.
As we are seeking a correction term for well anharmonicity,
it seems reasonable to truncate equation 3.19
and examine the effect of the first term in this series.
Laplace transformation then gives for the partition function
is the barrier height.
As we are seeking a correction term for well anharmonicity,
it seems reasonable to truncate equation 3.19
and examine the effect of the first term in this series.
Laplace transformation then gives for the partition function
| 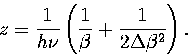 |
(3.20) |
The multi-dimensional partition function is then
| 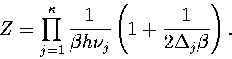 |
(3.21) |
Making the approximation that an average value of 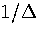 can be used then gives
can be used then gives
| 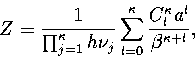 |
(3.22) |
where 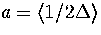 is an anharmonicity parameter and
is an anharmonicity parameter and 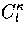 is a binomial coefficient.
Inverse Laplace transforming gives
is a binomial coefficient.
Inverse Laplace transforming gives
| 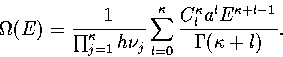 |
(3.23) |
The total density of states is found by summing over all the minima, giving
| 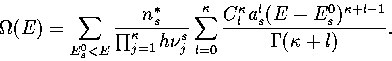 |
(3.24) |
Converting the above equation to the 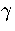 formulation using equation 3.7 gives
formulation using equation 3.7 gives
| ![\begin{displaymath}
\Omega(E)\propto\sum_{E^0_s<E}\gamma(E')_s\left[\sum_{l=0}^\...
...a_l a_s^l (E'-E^0_s)^{\kappa+l-1}\over\Gamma(\kappa+l)}\right].\end{displaymath}](img139.gif) |
(3.25) |
The temperature follows from equation 3.10
| ![\begin{displaymath}
T_\mu={\displaystyle{\sum_{E^0_s<E}\gamma(E')_s\left[\sum_{l...
..._l a_s^l(E'-E^0_s)^{\kappa+l-1}\over\Gamma(\kappa+l)}\right]}}.\end{displaymath}](img140.gif) |
(3.26) |
This anharmonic correction has a similar form to that used by Chekmarev and
Urmirzakov[165] but has been derived in a different way.
We consider two possible ways of calculating as from the
potential energy surface of LJ55. Firstly, we consider using the third
derivatives of the potential.
The dissociation energy of a one-dimensional Morse oscillator can be found from the
second and third derivatives of the potential by
| 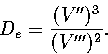 |
(3.27) |
If off-diagonal elements in the multidimensional case are ignored, the above
equation can be used to calculate the barrier heights associated with each normal mode.
Using analytical third derivatives of the LJ potential,
the Cartesian third derivatives for the LJ55 icosahedron were calculated
and transformed to obtain the diagonal elements in the Hessian eigenvector basis.
This scheme underestimates the anharmonicity and gives values for as which when substituted
into equation 3.26 have an insignificant effect on 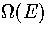 , because the off-diagonal elements,
which far outnumber the diagonal elements, should not be neglected.
However, there is no obvious way to calculate the effect of the off-diagonal elements
and for a system such as LJ55 the transformation of the third derivatives
into the Hessian eigenvector basis is too computationally expensive for the
off-diagonal elements.
, because the off-diagonal elements,
which far outnumber the diagonal elements, should not be neglected.
However, there is no obvious way to calculate the effect of the off-diagonal elements
and for a system such as LJ55 the transformation of the third derivatives
into the Hessian eigenvector basis is too computationally expensive for the
off-diagonal elements.
The second method considered was to use the barrier heights of our transition
state sample.
An average barrier height was
calculated for each minimum, but for some minima it led to a gross
overestimation of the anharmonicity and unphysical caloric curves. The
barrier heights are not a good quantitative measure of
the anharmonicity of an individual minimum. This method was therefore not
considered further.
Therefore, instead of trying to obtain as from the PES, we considered how
it could be obtained by comparison with the simulation results.
If as is assumed to be the same for all minima,
a value of a can be found which leads to the reproduction of the
Van der Waals loop in the caloric curve at the observed temperature and energy,
but the temperature difference between the two turning points is still too small.
However, one would expect the anharmonicity to depend upon the energy of the minimum: the higher energy minima
are likely to have a greater anharmonicity than the solid-like minima.
Table 3.5:
Values of the anharmonicity parameter, ai, for LJ55 in
the six energy ranges given in Table 3.1.
Values for I,
II,
III and
VI
were found by fitting the temperatures for these regions to the simulation results.
 |
In §3.3, we saw an example of how the properties of different regions of
configuration space could be obtained using suitable order parameters.
Indeed, for LJ55, the caloric curves associated with minima in different
energy ranges were found.
Using the superposition method, it is easy to calculate the properties of
a particular region of configuration space simply by restricting the summation to
those minima with suitable values of an order parameter, i.e.
| 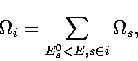 |
(3.28) |
where 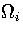 is the densities of states associated with region i.
From the definition,
is the densities of states associated with region i.
From the definition, 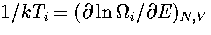 , where Ti
is the temperature of region i, it follows that
, where Ti
is the temperature of region i, it follows that
| ![\begin{displaymath}
T_i={\displaystyle{\sum_{E^0_s<E, s\in i}\gamma(E')_s\left[\...
..._l a_s^l(E'-E^0_s)^{\kappa+l-1}\over\Gamma(\kappa+l)}\right]}}.\end{displaymath}](img146.gif) |
(3.29) |
We assigned values of the anharmonicity parameter, ai,
to minima in the six different energy ranges (Table 3.1).
Values were chosen for regions
I, II,
III and
VI
which reproduced the simulation results of Figure 3.4.
The caloric curves for each region accurately fitted the simulation curves showing
that our anharmonic correction term has an appropriate form.
Values of ai for regions IV
and V were chosen that were
intermediate between the values for regions
III and
VI, but as these regions only make a small contribution to 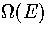 the
exact value chosen will only have a very small effect on the overall caloric curve.
The values of ai are given in Table 3.5.
As would be expected the anharmonicity increases with the potential energy of the minima.
the
exact value chosen will only have a very small effect on the overall caloric curve.
The values of ai are given in Table 3.5.
As would be expected the anharmonicity increases with the potential energy of the minima.
Figure 3.7:
Microcanonical caloric curves for LJ55 using
the 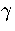 formula including anharmonic terms with minima samples A (solid line) and B (dashed line).
The calculated caloric curves are compared to simulation (dashed line with diamonds).
formula including anharmonic terms with minima samples A (solid line) and B (dashed line).
The calculated caloric curves are compared to simulation (dashed line with diamonds).
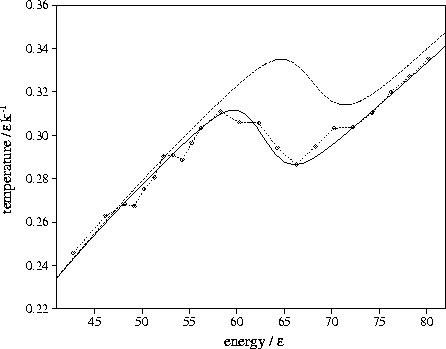 |
The microcanonical caloric curve was calculated using these values of ai.
Figure 3.7 shows that for sample A the calculated curve is in remarkable agreement with
the simulation results. The calculated Van der Waals loop now has the correct depth, because
the effect of the greater anharmonicity of the liquid-like state is to increase
the difference in temperature between the two branches of the caloric curve.
The success of this method can be understood from the equation
| 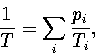 |
(3.30) |
where pi is the probability that the cluster is in region i.
The probabilities at E', pi(E') are fixed by the quench frequencies,
| 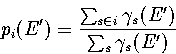 |
(3.31) |
Furthermore, the pi calculated from sample A are in good agreement
with simulation results over a wide range of energy (see §3.6).
The values of ai have been chosen to reproduce the simulation temperatures, Ti,
and so it is unsurprising that the overall temperature, T, is
very accurate. Sample B produces worse results because there are fewer
quenches to regions 1-3,
and so the quench frequencies are subject to larger statistical errors than for sample A.
For LJ13, the STA temperature distribution is bimodal. The high temperature
peak corresponds to solid-like clusters associated with the icosahedral
global minimum, and the low temperature peak to liquid-like clusters. The
residence times in the solid-like and liquid-like states are much shorter than
for LJ55 and so the information provided by short-time averaging
for LJ13 is less well-resolved. We partitioned the
minima distribution into these two regions, and assigned values of ai
to each. The values of ai were higher than for LJ55 and the
curvature of the Ti curves differed from the simulation results. The
apparently greater anharmonicity can be explained by the larger number of surface
atoms for LJ13. The incorrect curvature suggests that the energy dependence of
the density of states is inappropriate and so the 2nd-order Morse correction
term to the density of states was included. The resulting Ti curves
fitted the simulation results much more accurately. The partition function for
a single minimum including this term is
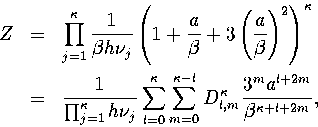
(3.32)
(3.33)
where
| 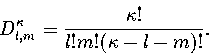 |
(3.34) |
Inverse Laplace transforming and summing over all minima gives for the total density of states,
| 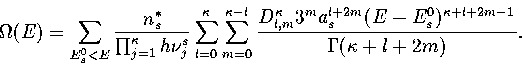 |
(3.35) |
In an MD simulation one calculates the kinetic temperature, TK.
For LJ55 the difference between the thermodynamic and kinetic temperatures is negligible.
For LJ13 it is still small but not insignificant,
and so TK rather than 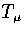 is fitted to the simulation results.
Bixon and Jortner found both temperatures produced very similar results
in their model calculations of the microcanonical caloric curve[152].
TK has been obtained for the harmonic superposition method by Franke
using the equipartition theorem[154],
however this approach cannot be extended to include anharmonicity.
We obtain TK by a different method.
Firstly we note that
is fitted to the simulation results.
Bixon and Jortner found both temperatures produced very similar results
in their model calculations of the microcanonical caloric curve[152].
TK has been obtained for the harmonic superposition method by Franke
using the equipartition theorem[154],
however this approach cannot be extended to include anharmonicity.
We obtain TK by a different method.
Firstly we note that
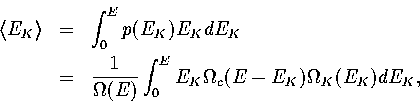
(3.36)
(3.37)
where 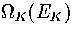 is the kinetic density of states,
is the kinetic density of states, 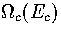 is
the configurational density of states, and the potential energy Ec is
given by Ec=E-EK.
Deconvoluting
is
the configurational density of states, and the potential energy Ec is
given by Ec=E-EK.
Deconvoluting 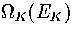 from
from 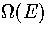 gives
gives
| 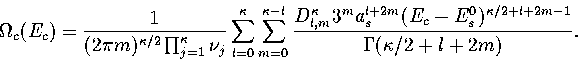 |
(3.38) |
Integrating equation 3.37, summing over all minima
and substituting into equation 3.3 gives
| 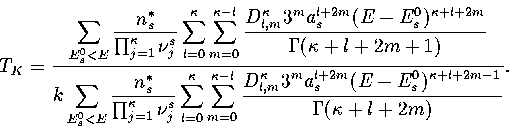 |
(3.39) |
Table 3.6:
Details of the two samples of minima for LJ13. E' is
measured with respect to the global minimum icosahedron.
| |
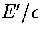 |
Number of minima |
| C |
13.7768 |
95 |
| D |
18.3268 |
295 |
Table 3.7:
Values of the anharmonicity parameter, ai,
for the solid-like (1)
and liquid-like (2) regions of the LJ13 PES.
Region I is the potential well of the icosahedron
and region II consists of all other minima.
| Region |
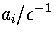 |
| I |
0.470 |
| II |
0.625 |
Sample C (Table 3.6) was used to calculate
the caloric curve of LJ13 for the 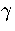 formulation
because it was produced from an MD run in the coexistence region and so should have more accurate quench
statistics for the low energy minima, and sample D was used for the n* formulation because it is from the
liquid-like region and so has a larger sample of minima.
The values of ai assigned to solid-like and liquid-like clusters
are given in Table 3.7.
From Figure 3.8 it can be seen that the
caloric curve given by the n* formulation agrees very well with
simulation, because it is possible to obtain a near-complete set
of minima for LJ13.
(Tsai and Jordan found 1328 minima in a comprehensive search of the LJ13 PES[162].
Many of these, though, are too high in energy to be thermodynamically significant.)
The
formulation
because it was produced from an MD run in the coexistence region and so should have more accurate quench
statistics for the low energy minima, and sample D was used for the n* formulation because it is from the
liquid-like region and so has a larger sample of minima.
The values of ai assigned to solid-like and liquid-like clusters
are given in Table 3.7.
From Figure 3.8 it can be seen that the
caloric curve given by the n* formulation agrees very well with
simulation, because it is possible to obtain a near-complete set
of minima for LJ13.
(Tsai and Jordan found 1328 minima in a comprehensive search of the LJ13 PES[162].
Many of these, though, are too high in energy to be thermodynamically significant.)
The 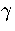 formulation, however, has too high a transition temperature.
This error arises because the probability that the
cluster is in the solid-like state derived from quenching is
higher than the corresponding probability derived from the STA
temperature distributions. In the
formulation, however, has too high a transition temperature.
This error arises because the probability that the
cluster is in the solid-like state derived from quenching is
higher than the corresponding probability derived from the STA
temperature distributions. In the 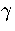 formulation the probabilities, pi, at E' are
fixed by the quench statistics (equation 3.31),
and so this constraint leads to the higher transition temperature.
The difference between the probabilities derived from quenching and the STA
temperature distributions may be because
there are regions of the PES which are in the basin of
attraction of the icosahedron but which have thermodynamic properties
similar to a liquid-like well, or because the short-time averaging does not
distinguish between the solid-like and liquid-like states with the same resolution as for LJ55.
This difference does not stem from the
quench method since we obtained similar quench statistics with
steepest-descent[170,171], conjugate gradient[87]
and eigenvector-following[88] methods.
formulation the probabilities, pi, at E' are
fixed by the quench statistics (equation 3.31),
and so this constraint leads to the higher transition temperature.
The difference between the probabilities derived from quenching and the STA
temperature distributions may be because
there are regions of the PES which are in the basin of
attraction of the icosahedron but which have thermodynamic properties
similar to a liquid-like well, or because the short-time averaging does not
distinguish between the solid-like and liquid-like states with the same resolution as for LJ55.
This difference does not stem from the
quench method since we obtained similar quench statistics with
steepest-descent[170,171], conjugate gradient[87]
and eigenvector-following[88] methods.
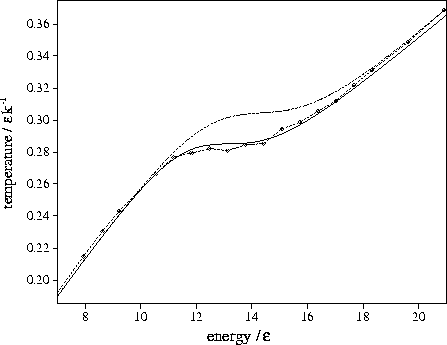
Figure 3.8:
Microcanonical caloric curves for LJ13 using the n* formula (solid
line), the 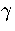 formula (dashed line) and from simulation (dashed line with diamonds).
Both the n* and
formula (dashed line) and from simulation (dashed line with diamonds).
Both the n* and 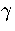 formula curves include anharmonic terms.
formula curves include anharmonic terms.
 |



Next: Thermodynamic Properties
Up: Anharmonicity
Previous: The effect of transition
Home: Return to my homepage
Jon Doye
8/27/1997
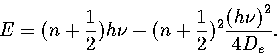
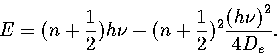
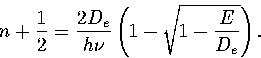
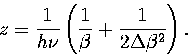
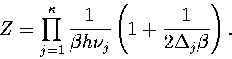
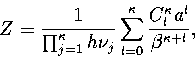
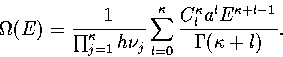
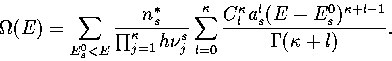
![\begin{displaymath}
\Omega(E)\propto\sum_{E^0_s<E}\gamma(E')_s\left[\sum_{l=0}^\...
...a_l a_s^l (E'-E^0_s)^{\kappa+l-1}\over\Gamma(\kappa+l)}\right].\end{displaymath}](img139.gif)
![\begin{displaymath}
T_\mu={\displaystyle{\sum_{E^0_s<E}\gamma(E')_s\left[\sum_{l...
..._l a_s^l(E'-E^0_s)^{\kappa+l-1}\over\Gamma(\kappa+l)}\right]}}.\end{displaymath}](img140.gif)
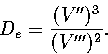

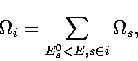
![\begin{displaymath}
T_i={\displaystyle{\sum_{E^0_s<E, s\in i}\gamma(E')_s\left[\...
..._l a_s^l(E'-E^0_s)^{\kappa+l-1}\over\Gamma(\kappa+l)}\right]}}.\end{displaymath}](img146.gif)

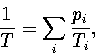
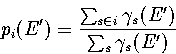
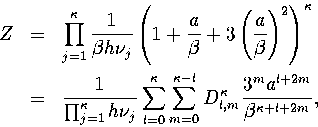
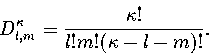
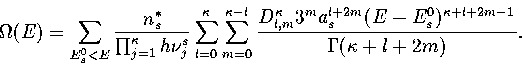
![]() is fitted to the simulation results.
Bixon and Jortner found both temperatures produced very similar results
in their model calculations of the microcanonical caloric curve[152].
TK has been obtained for the harmonic superposition method by Franke
using the equipartition theorem[154],
however this approach cannot be extended to include anharmonicity.
We obtain TK by a different method.
Firstly we note that
is fitted to the simulation results.
Bixon and Jortner found both temperatures produced very similar results
in their model calculations of the microcanonical caloric curve[152].
TK has been obtained for the harmonic superposition method by Franke
using the equipartition theorem[154],
however this approach cannot be extended to include anharmonicity.
We obtain TK by a different method.
Firstly we note that
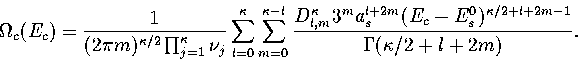
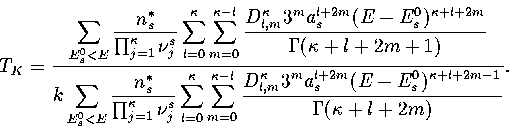
![]() formulation
because it was produced from an MD run in the coexistence region and so should have more accurate quench
statistics for the low energy minima, and sample D was used for the n* formulation because it is from the
liquid-like region and so has a larger sample of minima.
The values of ai assigned to solid-like and liquid-like clusters
are given in Table 3.7.
From Figure 3.8 it can be seen that the
caloric curve given by the n* formulation agrees very well with
simulation, because it is possible to obtain a near-complete set
of minima for LJ13.
(Tsai and Jordan found 1328 minima in a comprehensive search of the LJ13 PES[162].
Many of these, though, are too high in energy to be thermodynamically significant.)
The
formulation
because it was produced from an MD run in the coexistence region and so should have more accurate quench
statistics for the low energy minima, and sample D was used for the n* formulation because it is from the
liquid-like region and so has a larger sample of minima.
The values of ai assigned to solid-like and liquid-like clusters
are given in Table 3.7.
From Figure 3.8 it can be seen that the
caloric curve given by the n* formulation agrees very well with
simulation, because it is possible to obtain a near-complete set
of minima for LJ13.
(Tsai and Jordan found 1328 minima in a comprehensive search of the LJ13 PES[162].
Many of these, though, are too high in energy to be thermodynamically significant.)
The ![]() formulation, however, has too high a transition temperature.
This error arises because the probability that the
cluster is in the solid-like state derived from quenching is
higher than the corresponding probability derived from the STA
temperature distributions. In the
formulation, however, has too high a transition temperature.
This error arises because the probability that the
cluster is in the solid-like state derived from quenching is
higher than the corresponding probability derived from the STA
temperature distributions. In the ![]() formulation the probabilities, pi, at E' are
fixed by the quench statistics (equation 3.31),
and so this constraint leads to the higher transition temperature.
The difference between the probabilities derived from quenching and the STA
temperature distributions may be because
there are regions of the PES which are in the basin of
attraction of the icosahedron but which have thermodynamic properties
similar to a liquid-like well, or because the short-time averaging does not
distinguish between the solid-like and liquid-like states with the same resolution as for LJ55.
This difference does not stem from the
quench method since we obtained similar quench statistics with
steepest-descent[170,171], conjugate gradient[87]
and eigenvector-following[88] methods.
formulation the probabilities, pi, at E' are
fixed by the quench statistics (equation 3.31),
and so this constraint leads to the higher transition temperature.
The difference between the probabilities derived from quenching and the STA
temperature distributions may be because
there are regions of the PES which are in the basin of
attraction of the icosahedron but which have thermodynamic properties
similar to a liquid-like well, or because the short-time averaging does not
distinguish between the solid-like and liquid-like states with the same resolution as for LJ55.
This difference does not stem from the
quench method since we obtained similar quench statistics with
steepest-descent[170,171], conjugate gradient[87]
and eigenvector-following[88] methods.
