 |
 |
![[*]](foot_motif.gif) Kunz and Berry observed that the cluster would spend a period of time in one
region of configuration space, say with a single surface vacancy, and then jump
to a region with a different number of vacancies and a different characteristic
potential energy.
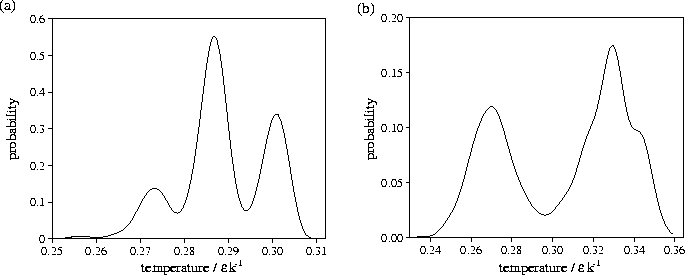
As a result, multimodality is seen in the probability distributions for the
microcanonical STA temperature. An example is shown in Figure 3.1a
where three coexisting states are seen.
As the STA temperature reflects the minimum energy of the wells with which the cluster is
associated (high temperatures correspond to low energy minima),
we expect that the STA temperature peaks will be related to features in the energy
distribution of minima (Figure 3.2).
Kunz and Berry observed that the cluster would spend a period of time in one
region of configuration space, say with a single surface vacancy, and then jump
to a region with a different number of vacancies and a different characteristic
potential energy.
As a result, multimodality is seen in the probability distributions for the
microcanonical STA temperature. An example is shown in Figure 3.1a
where three coexisting states are seen.
As the STA temperature reflects the minimum energy of the wells with which the cluster is
associated (high temperatures correspond to low energy minima),
we expect that the STA temperature peaks will be related to features in the energy
distribution of minima (Figure 3.2).
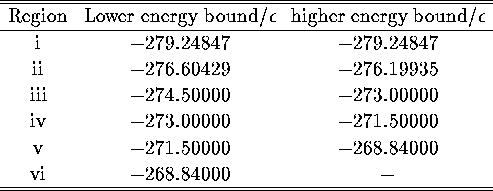
To test this hypothesis, quenches were performed from configurations generated by an MD run at the energy of Figure 3.1a if they had an STA temperature near to the maxima of any of the three peaks. The resulting minima were then assigned to one of the six energy ranges given in Table 3.1. The results, given in Table 3.2, unequivocally show the correspondence between the STA temperature peaks and the peaks in the potential energy probability distribution for minima. Therefore the STA temperature can be used to elucidate the connection between the observed behaviour and local minima on the PES.
 |
| Lower | Upper | Number of | ||||
| Temperature | Temperature | quenches | I | II | III | IV and V |
| 0.3047 | 0.3050 | 110 | 110 | |||
| 0.2909 | 0.2912 | 72 | 2 | 70 | ||
| 0.2756 | 0.2785 | 86 | 1 | 9 | 74 | 2 |
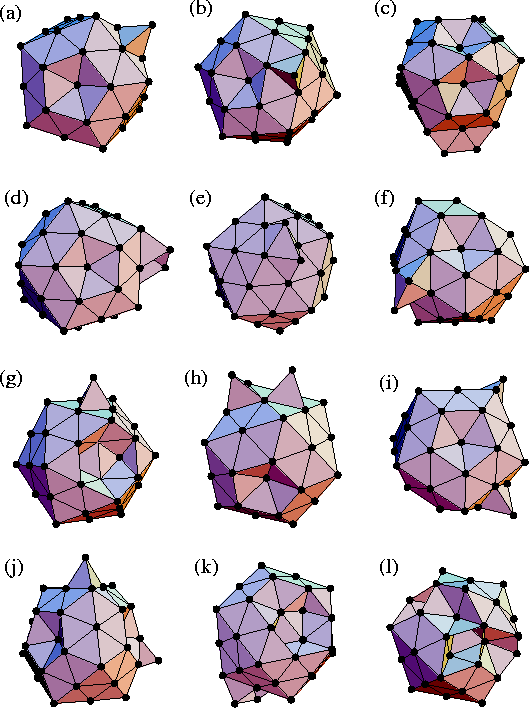 |
The highest temperature peak corresponds to the Mackay icosahedral global minimum, but to assign sets of structures to the other peaks, some of the minima in energy ranges II and III were examined further. Range II consists of icosahedral-based structures with a vacancy in a five-coordinate vertex site and a single adatom. There are eleven such structures, four with the adatom in the centre of a triangular face (Figure 3.3a) and seven with the adatom in an off-centre site (Figure 3.3b). These structures have been reported previously in a study using a more sophisticated potential to represent Ar[108]. Range III consists of structures with two vertex vacancies and two adatoms (Figure 3.3c-f and h-j), and structures with a vacancy in a six-coordinate edge site and a single adatom (Figure 3.3g). For the lower energy structures in this range, the two adatoms form a pair, either on the same face (Figure 3.3c and d) or straddling two faces (Figure 3.3e and f). We also examined some minima corresponding to range IV. We found structures with three adatoms, as well as some with adjacent edge and vertex vacancies and two adatoms (Figure 3.3k) and more complicated distorted icosahedra (Figure 3.3l).
| Label | Description | PG | Energy/ |
| a | vertex vacancy + centred adatom | Cs | -276.59676 |
| b | vertex vacancy + off-centred adatom | C1 | -276.19935 |
| c | 2 vertex vacancies + adatom pair | Cs | -274.28136 |
| d | 2 vertex vacancies + adatom pair | C1 | -274.25058 |
| e | 2 vertex vacancies + adatom pair | C1 | -274.21687 |
| f | 2 vertex vacancies + adatom pair | C1 | -274.13672 |
| g | edge vacancy + centred adatom | Cs | -274.08950 |
| h | 2 vertex vacancies + 2 adatoms | C1 | -273.83234 |
| i | 2 vertex vacancies + 2 adatoms | C1 | -273.62356 |
| j | 2 vertex vacancies + 2 adatoms | C1 | -273.21257 |
| k | fused vertex and edge vacancy + adatom pair | C1 | -272.82603 |
| l | distorted icosahedron | Cs | -272.58659 |
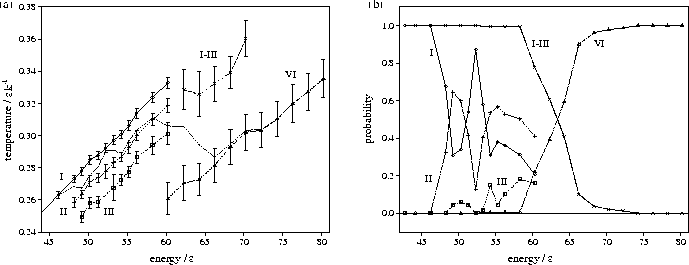
The STA temperature distributions were partitioned according to their peaks,
and the mean and standard deviation of the temperature were
calculated for each, along with the integrated probabilities.
This allows the caloric curves for restricted regions of the configuration space
to be obtained (Figure 3.4a).
Regions 2 and 3
have a small effect on the caloric curve; they cause it to bend gradually away from
the temperature corresponding to the Mackay icosahedron alone.
From the probabilities (Figure 3.4b) it can be seen that, despite their length,
some of the MD runs have not achieved ergodicity in the energy range ![]() .
This is because the free energy barriers between the different states can be large, and so
passage between the different states can be infrequent on the time scale of the run.
.
This is because the free energy barriers between the different states can be large, and so
passage between the different states can be infrequent on the time scale of the run.
 |