 |
The 38-atom truncated octahedron is the most stable fcc cluster in the size range we consider.
It becomes the global minimum at the lowest value of ![]() (4.76) of any of the close-packed structures.
Curiously, there are two ranges of
(4.76) of any of the close-packed structures.
Curiously, there are two ranges of ![]() for which it is the global minimum.
At long range, Ennn represents a significant part of the total energy.
The truncated octahedron is most stable for
for which it is the global minimum.
At long range, Ennn represents a significant part of the total energy.
The truncated octahedron is most stable for ![]() because it is approximately spherical
and so has a larger value of Ennn than the more oblate icosahedral structure 38E.
For shorter-ranged potentials, the contribution of Ennn diminishes and so 38E becomes
the global minimum for
because it is approximately spherical
and so has a larger value of Ennn than the more oblate icosahedral structure 38E.
For shorter-ranged potentials, the contribution of Ennn diminishes and so 38E becomes
the global minimum for ![]() because it has a larger nnn.
Then for
because it has a larger nnn.
Then for ![]() the truncated octahedron again becomes the global minimum because it has
a lower strain energy than 38E.
There is a growing body of experimental evidence for the importance of truncated octahedra.
EXAFS (extended x-ray absorption fine structure) spectra of small gold clusters
suggest that truncated octahedral clusters are present,
particularly the 38-atom truncated octahedron[101].
Gold clusters passivated by alkylthiolate molecules selectively form truncated
octahedra, which can even be isolated and formed into superlattices[7].
The structure is also observed for ligated 38-atom platinum clusters[5].
the truncated octahedron again becomes the global minimum because it has
a lower strain energy than 38E.
There is a growing body of experimental evidence for the importance of truncated octahedra.
EXAFS (extended x-ray absorption fine structure) spectra of small gold clusters
suggest that truncated octahedral clusters are present,
particularly the 38-atom truncated octahedron[101].
Gold clusters passivated by alkylthiolate molecules selectively form truncated
octahedra, which can even be isolated and formed into superlattices[7].
The structure is also observed for ligated 38-atom platinum clusters[5].
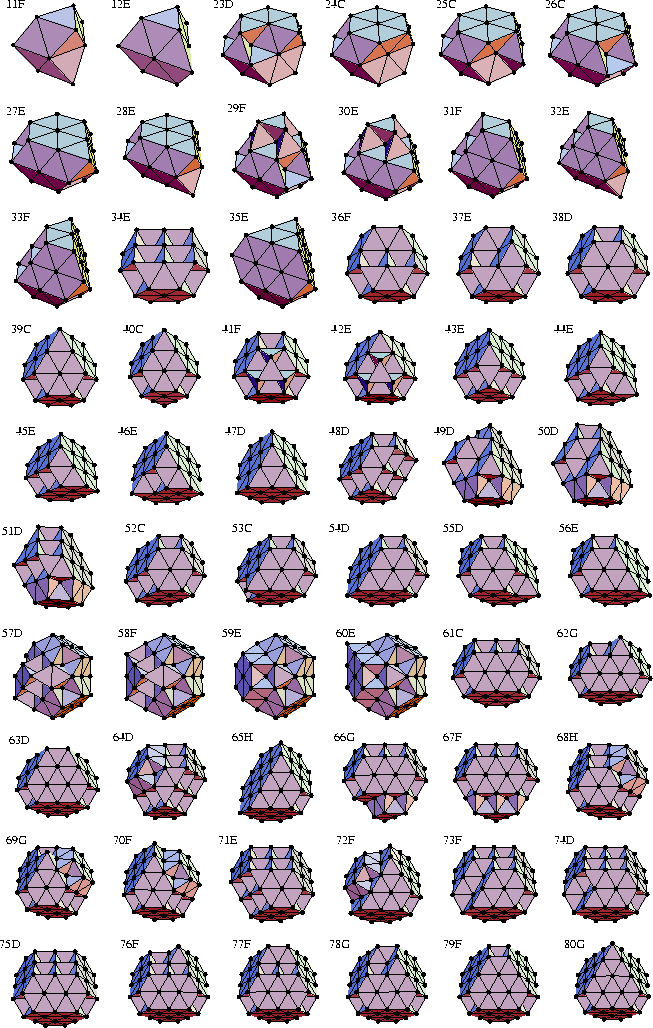
Most of the structures with between 38 and 79 atoms are broadly based on a growth sequence
that goes between the two truncated octahedra.
It proceeds by addition of overlayers to four of the ![]() faces and
by capping any new (
faces and
by capping any new (![]() )
) ![]() faces created.
For example, there is a peak in
faces created.
For example, there is a peak in ![]() at
at ![]() that is caused by the low energy of 52C;
this structure is formed by the addition of complete overlayers to two faces of 38D.
For a number of sizes, the structures that result from adding the overlayers in fcc or hcp sites
with respect to
that is caused by the low energy of 52C;
this structure is formed by the addition of complete overlayers to two faces of 38D.
For a number of sizes, the structures that result from adding the overlayers in fcc or hcp sites
with respect to ![]() faces have the same nnn.
For these cases the structures with the hcp overlayers are often lower in energy
because they have a larger value of Ennn--some of the third
nearest neighbours are at 1.63 rather than 1.73 times the equilibrium pair separation.
Examples include 41F, 42C, 64D, 66G, 67F, 68H, 69G, 70F and 72F.
faces have the same nnn.
For these cases the structures with the hcp overlayers are often lower in energy
because they have a larger value of Ennn--some of the third
nearest neighbours are at 1.63 rather than 1.73 times the equilibrium pair separation.
Examples include 41F, 42C, 64D, 66G, 67F, 68H, 69G, 70F and 72F.
The exceptions to the above growth sequence are those structures--49D, 50D, 51D, 57D, 58F and 60E--that
are based on structure 59D.
This structure is a 31-atom truncated tetrahedron with the faces covered by four seven-atom hexagonal
overlayers occupying hcp sites with respect to the underlying tetrahedron.
The smaller of those structures based on 59D have no overlayer on one face of the underlying tetrahedron.
The stability of 59D comes from the combination of its high proportion
of ![]() faces and spherical shape.
Interestingly, if atoms are added to one of the grooves in the structure a decahedral-like
axis results, suggesting a possible transformation route between decahedral and closed-packed clusters.
faces and spherical shape.
Interestingly, if atoms are added to one of the grooves in the structure a decahedral-like
axis results, suggesting a possible transformation route between decahedral and closed-packed clusters.
It is worth noting that the cuboctahedron is not the lowest energy close-packed structure for N=55. In fact, it has five fewer nearest neighbours than structure 55D. Consequently, one has interpret with caution those studies in which cuboctahedra have been compared with Mackay icosahedra[75,102,103,104]; the cuboctahedra are likely to be suboptimal fcc structures, thus making the comparison unfair.