A Note on Units and Planck's Constant

Aside from CHARMM and AMBER OPTIM does no unit conversions. These systems are treated differently, as explained below. For all other cases PATHSAMPLE is expecting to receive $\ln\Pi_i \omega^2_i$ in the min.data and ts.data files. PATHSAMPLE converts $\omega$ to $\nu$ using $\nu=\omega/2\pi$, but also does no unit conversions. The rate constants are therefore in natural frequency units of $\sqrt{\epsilon/m\sigma^2}$, where $\epsilon$ is the unit of energy, $m$ is the unit of mass, and $\sigma$ is the unit of length.

For a system where all particles have equal masses, $m$, the rate constants calculated by PATHSAMPLE can therefore be converted to SI units by multiplying by $\sqrt{(\epsilon/{\rm J})/(m/{\rm kg})(\sigma/{\rm m})^2}$.

For calculations involving free energy regrouping schemes we need to supply a value for the Planck constant in reduced units via the PLANCK keyword. Since the temperature is read in energy units, i.e. $\epsilon$, so that $k_BT$ is in $\epsilon$, we need to define $h$ in reduced units so that terms like $k_BT/h\nu$ are dimensionless. If $\nu$ is in reduced time units then we need $(h/{\rm Js})$ divided by the unit of energy and the unit of time. The reduced value of $h$ is therefore

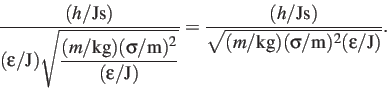$$\frac{(h/{\rm Js})}{(\epsilon/{\rm J}) \sqrt{\displaystyle\f... ...s})}{\sqrt{(m/{\rm kg})(\sigma/{\rm m})^2(\epsilon/{\rm J})}}.$$ (1)

For CHARMM and AMBER we need to diagonalise the reciprocal mass-weighted Hessian in OPTIM, where the various masses are known. For convenience the frequency unit conversion is done in OPTIM as well, so that the rate constants calculated in PATHSAMPLE are in s$^{-1}$ and do not need to be converted. The value required for the Planck constant is therefore different because $\nu$ is not in reduced units. Instead, we need to convert $(h/{\rm Js})(\nu/{\rm s}^{-1})$ to kcal/mol, since these are the units of $k_BT$. Hence we need $(h/{\rm Js})/(\epsilon/{\rm J})$, where $\epsilon$ is one kcal/mol. Since 1kcal/mol is $6.948\times10^{-21}\,$J the required value for the PLANCK keyword in regrouping calculations is $6.626\times10^{-34}/6.948\times10^{-21}=9.536\times10^{-14}$.