Basin-Sampling using HISTOGRAM and TETHER

The `basin-sampling' algorithm as described by Bogdan, Wales and Calvo [#!BogdanWC06!#] combines the `basin-hopping' [#!walesd97a!#] and Wang-Landau sampling techniques [#!wangl01!#] to study the thermodynamics of the transformed PES. It provides a direct temperature-independent estimate of the total energy density of states, along with thermodynamic properties such as the free energy and entropy via ensemble averages using samples of local minima, rather than instantaneous configurations.

In the GMIN implementation setting TEMPERATURE to zero and specifying the keyword HISTOGRAM invoke a `basin-sampling' run.

In the microcanonical `basin-sampling' procedure we start from a random configuration and perform a random walk in energy space by perturbing and minimising the structures. Assuming that a given energy is visited with probability reciprocal to the true density of states, we obtain a flat energy distribution. To restrict the search of configuration space to bound clusters, the structures are confined to a spherical container. For every visited state the current estimate of the energy density of local minima is updated by a multiplicative modification factor f (histfac). Acting as a convergence parameter, f is relatively large at first to allow for fast accumulation of the histograms over the full energy range, and over time it is self-consistently reduced towards unity. The length of one WL iteration, over which the value of the modification factor stays the same, is regulated by the `flatness parameter' x% (hpercent)—the percentage by which histogram entries are allowed to deviate from the mean. As f approaches a predefined value f_final (histfacmin), and provided the random walk is unbiased and all the energy levels are sampled uniformly, the energy density of local minima converges to its true value. If the VISITPROP keyword is specified, the convergence of one WL iteration is governed by the number of visits being proportional to 1/$\sqrt{(}$ln(f ))[#!ZhouB03!#].

The energy spectrum in question is bounded from below by the potential energy of the global minimum histmin and is separated into hbins equally spaced energy windows, which constitute histogram bins of width histint.

For a random configuration the probability of quenching to a minimum with potential energy lying in a given bin i is g_i = p_iA_i, where p_i is the probability of a random minimum having potential energy in a given bin, and A_i is the average configuration space volume of a basin of attraction for minima in this range. In the original basin-sampling study A_i is approximated by 〈D_i〉^κ, where 〈D_i〉 is the mean distance of a random starting point to the quenched minimum in the corresponding bin, and κ is the number of vibrational degrees of freedom.

During the random walk we accumulate g_i (the density of local minima in each bin—hweight), H_j and 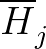$\overline{{H}}_{j}^{}$ (the global energy histogram histvals and the local energy histogram lhistvals, i.e. the number of visits in a given energy bin during one WL iteration), and 〈D_j〉 (hdist), which is updated when a new quenched minimum is added to the corresponding bin.

The run is started from a uniform energy distribution, g_i, and samples the configuration space with a probability inversely proportional to g_i. At each step all the Cartesian coordinates are displaced by a random number in the range [- 1, 1] times STEP. The structure obtained after each geometrical perturbation is then minimised using the modified limited memory Broyden-Fletcher-Goldfarb-Shanno (L-BFGS) algorithm[#!lbfgs!#]. In the case of an atom leaving the container at any point the coordinates are reset to the starting geometry, and the previous minimum is recounted. If the minimisation is successful, the weights of the bins to which the starting (i) and the quenched (i^′) minima belong are compared . If g_i > g_i', the density of states of the i^′-th bin is updated as g_i'→g_i'f, its energy histograms are incremented as H_i'→H_i' + 1 and 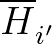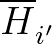$\overline{{H}}_{{i'}}^{}$→$\overline{{H}}_{{i'}}^{}$ + 1, and the distance between the starting and the quenched geometries is used to update 〈D_i'〉. If g_i < g_i' the attributes of the i-th bin are modified instead. If the walk goes outside the defined energy range we recount the structure in the i-th bin to avoid boundary effects. After updating the histogram we do not reset the coordinates at each successful step to those of the quenched minimum but allow the geometry to vary continuously. The opposite strategy is generally found to be more effective for global optimisation, but here we must maintain detailed balance.

The energy histograms are periodically checked against the convergence criterion . Because the energy spectrum is discrete some energy bins may never be visited. Also, to prevent trapping when f is close to f_final, bins where H_i has fewer than 5% of the average number of entries are ignored by setting the ignorebin flag to true. When the non-zero parts of the histogram are considered sufficiently flat, the modification factor is reduced using a square root function, the values of 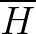$\overline{{H}}$ are reset and another WL iteration is started. The final statistical weights, g_i, can be used to calculate the canonical partition function in terms of contributions from the catchment basins in each energy range i.

The geometries of minima can be saved along the run by specifying BINSTRUCTURES keyword. Keyword EQUILIBRATION regulates the starting point and frequency of recording statistics.

The output of the `basin-sampling' run is printed in BL.Pjnorm.lnGj.Djnm.Djm.VT.his in the following format: histmin+(i-1/2)⋅histint; hweight(i)⋅(distmin/dist(i))^κ normalised to 1; 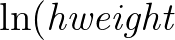$\it\ln(hweight$(i)) normalized to 1; average hdist(i) minimised with respect to rigid body coordinates; unminimised average hdist(i); histvals(i).

Calculation of the vibrational density of states for a given minimum is invoked by the additional TETHER keyword, which requests a conventional Wang-Landau sampling of the configuration space restricted to the average volume of the basin of attraction to which a given minimum belongs.[#!BogdanWC06!#]