


Next: Coulomb
Up: Potentials
Previous: Potentials
Contents
[classi] [classj] lj [sigma_0] [epsilon_0] [rep] [att]
Here A is the repulsive coefficient and B is the attractive coefficient.
For a typical LJ usage, set A = B = 1. For a purely repulsive LJ site, set A = 1 and B = 0. Some potentials (e.g., TIP4P) use values of A and B that
are both not equal to 1.
 A
A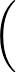
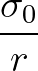
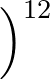 - B
- B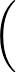
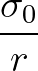
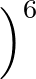
![$\displaystyle \left.\vphantom{ A \left(\frac{\sigma_0}{r}\right)^{12} - B \left(\frac{\sigma_0}{r}\right)^6}\right]$](img126.png)
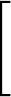 A
A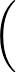
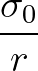
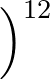 - B
- B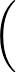
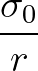
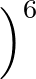
![$\displaystyle \left.\vphantom{ A \left(\frac{\sigma_0}{r}\right)^{12} - B \left(\frac{\sigma_0}{r}\right)^6}\right]$](img126.png)