| V | = |  Kr Kr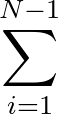 (Ri, i+1 - Re)2 + (Ri, i+1 - Re)2 +  Kθ Kθ (θi - θe)2 (θi - θe)2 |
|
+ ε 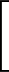 Ai(1 + cos Ai(1 + cos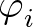 ) + Bi(1 - cos ) + Bi(1 - cos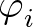 ) ) |
|||
+ Ci(1 + cos 3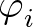 ) + Di ) + Di![$\displaystyle \left(\vphantom{1+\cos\left[\varphi_i+\pi/4\right]}\right.$](img84.png) 1 + cos 1 + cos 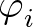 + π/4 + π/4![$\displaystyle \left.\vphantom{\varphi_i+\pi/4}\right]$](img86.png) ![$\displaystyle \left.\vphantom{1+\cos\left[\varphi_i+\pi/4\right]}\right)$](img87.png) ![$\displaystyle \Big]$](img88.png) |
|||
+ 4ε 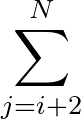  S12 S12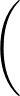 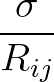 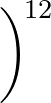 + S6 + S6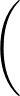 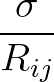 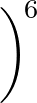 ![$\displaystyle \left.\vphantom{S_{12}\left(\frac{\sigma}{R_{ij}}\right)^{\!12}
+S_6\!\left(\frac{\sigma}{R_{ij}}\right)^{\!6}}\right]$](img96.png) , , |
(9) |
The general three-colour bead protein model is specified by keyword BLN. The potential follows the form described in Proc. Natl. Acad. Sci. USA, 100, 10712, 2003, expect that the coefficients Ai, Bi, Ci and Di include a factor of ε explicitly.
0pt
| V | = |  Kr Kr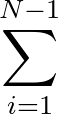 (Ri, i+1 - Re)2 + (Ri, i+1 - Re)2 +  Kθ Kθ (θi - θe)2 (θi - θe)2 |
|
+ ε 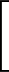 Ai(1 + cos Ai(1 + cos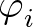 ) + Bi(1 - cos ) + Bi(1 - cos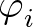 ) ) |
|||
+ Ci(1 + cos 3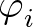 ) + Di ) + Di![$\displaystyle \left(\vphantom{1+\cos\left[\varphi_i+\pi/4\right]}\right.$](img84.png) 1 + cos 1 + cos 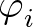 + π/4 + π/4![$\displaystyle \left.\vphantom{\varphi_i+\pi/4}\right]$](img86.png) ![$\displaystyle \left.\vphantom{1+\cos\left[\varphi_i+\pi/4\right]}\right)$](img87.png) ![$\displaystyle \Big]$](img88.png) |
|||
+ 4ε 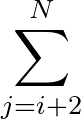  S12 S12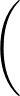 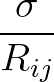 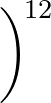 + S6 + S6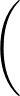 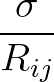 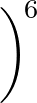 ![$\displaystyle \left.\vphantom{S_{12}\left(\frac{\sigma}{R_{ij}}\right)^{\!12}
+S_6\!\left(\frac{\sigma}{R_{ij}}\right)^{\!6}}\right]$](img96.png) , , |
(9) |
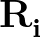 to
to
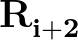 , and values
Kθ = 20 ε rad-2 and
θe = 105o were
used for the 46-bead model.
The third term
is a sum over the dihedral angles,
, and values
Kθ = 20 ε rad-2 and
θe = 105o were
used for the 46-bead model.
The third term
is a sum over the dihedral angles, 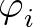 , defined by the quartets
, defined by the quartets 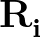 to
to
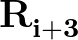 .
In the 46-bead model
Ai = Ci = 1.2 if the quartet involved no more than one N monomer, generating
a preference for the trans conformation (
.
In the 46-bead model
Ai = Ci = 1.2 if the quartet involved no more than one N monomer, generating
a preference for the trans conformation (
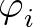 = 180o), whereas if two or three
N monomers are involved then Ai = 0 and Ci = 0.2.
This choice makes the three neutral
segments of the chain flexible and enables them to accommodate turns.
A general specification of these parameters is possible in the new BLN framework
via the auxiliary file BLNsequence.
The last term in (9) represents the nonbonded interactions.
In the current BLN implementation Re is set equal to σ, i.e. to
unity in reduced units.
= 180o), whereas if two or three
N monomers are involved then Ai = 0 and Ci = 0.2.
This choice makes the three neutral
segments of the chain flexible and enables them to accommodate turns.
A general specification of these parameters is possible in the new BLN framework
via the auxiliary file BLNsequence.
The last term in (9) represents the nonbonded interactions.
In the current BLN implementation Re is set equal to σ, i.e. to
unity in reduced units.
An appropriate BLNsequence file for the usual 46-bead model contains the following lines:
comment: S12 > 0 and S6 < 0 for B-B, L-L and L-B, N-L and N-B and N-N 1.0D0 -1.0D0 0.33333333333333D0 0.33333333333333D0 1.0D0 0.0D0 comment: coefficients A, B, C, D comment: for Helical, Extended and Turn residues in order, four per line 0.0D0 1.2D0 1.2D0 1.2D0 0.9D0 0.0D0 1.2D0 0.0D0 0.0D0 0.0D0 0.2D0 0.0D0 LBLBLBLBBNNNBBBLBLBBBNNNLLBLLBBLLBNBLBLBLBLNNNLBBLBLBBBL EEEEEETEHTHEEEEEEEEHHEHHHHHHHHHHEHTEEEEEEETTTEEEEEEEE
The penultimate line defines the sequence, and the final line defines which set of Ai, Bi, Ci and Di parameters apply to which parts of the structure.[33]